



suivant: Propriété d'incrémentalité de l'algorithme
monter: Résultats théoriques concernant l'algorithme
précédent: Convergence et prédictibilité de
Table des matières
L'algorithme CbL(1) possède un défaut important, dont
nous montrerons un exemple dans la section suivante. Un état
est marqué à 1 s'il existe une politique de commande fiable passant
par celui-ci. Or, pour le problème du labyrinthe (voir la section
suivante), beaucoup d'états du système sont inclus dans une politique
fiable menant à l'objectif. Cela signifie que beaucoup d'états ont
un marquage 1. En particulier, pour un même état, plusieurs actions
peuvent mener à un état de marquage 1. Dans ces conditions, quelle
action choisir ? L'algorithme de choix de l'action indique qu'il faut
en choisir une au hasard. On comprend dans ces conditions que le
marquage à 1 n'est pas très informatif parce qu'il ne permet pas de
diriger le système vers l'objectif.
L'algorithme CbL(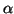 ) résout en partie cette difficulté en offrant
un ensemble fini de marquages intermédiaires entre le marquage 0 et le
marquage 1. L'invariant structurel force alors deux états de marquage
strictement positif, reliés par une transition, à posséder deux marquages
distincts. On peut alors ``remonter'' vers l'objectif grâce à l'algorithme
de choix d'action, en évitant l'utilisation permanente du hasard.
) résout en partie cette difficulté en offrant
un ensemble fini de marquages intermédiaires entre le marquage 0 et le
marquage 1. L'invariant structurel force alors deux états de marquage
strictement positif, reliés par une transition, à posséder deux marquages
distincts. On peut alors ``remonter'' vers l'objectif grâce à l'algorithme
de choix d'action, en évitant l'utilisation permanente du hasard.
D'un point de vue théorique, l'algorithme CbL(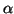 ) se
comporte de la même manière que CbL(1). La même qualité de
résultat peut être montrée pour des problèmes d'atteinte
d'objectif. Pour des problèmes de viabilité, les deux algorithmes
sont identiques. La valeur de
) se
comporte de la même manière que CbL(1). La même qualité de
résultat peut être montrée pour des problèmes d'atteinte
d'objectif. Pour des problèmes de viabilité, les deux algorithmes
sont identiques. La valeur de 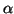 , pour
, pour
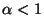 ,
n'influence aucunement le résultat de l'algorithme, c'est-à-dire
la politique de commande obtenue.
,
n'influence aucunement le résultat de l'algorithme, c'est-à-dire
la politique de commande obtenue.




suivant: Propriété d'incrémentalité de l'algorithme
monter: Résultats théoriques concernant l'algorithme
précédent: Convergence et prédictibilité de
Table des matières
2002-03-01