



suivant: Découverte de l'ajout d'une
monter: Propriété d'incrémentalité de l'algorithme
précédent: Qu'entendons-nous par ``incrémentalité'' ?
Table des matières
Nous savons que, dès que le système se trouve dans un état de
qualité strictement positive, le mécanisme de choix d'action lui
permet de se guider à coup sûr vers un objectif (rattaché à l'état
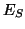 ). Cela n'est vrai que si le contexte respecte la propriété
(
). Cela n'est vrai que si le contexte respecte la propriété
(
 ). Nous supposons que cette propriété est
satisfaite. Dans ce cadre, si un état
). Nous supposons que cette propriété est
satisfaite. Dans ce cadre, si un état  du système possède
une transition vers
du système possède
une transition vers 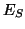 , nous savons que cette transition est
unique. Donc, si une nouvelle transition vers un état différent de
, nous savons que cette transition est
unique. Donc, si une nouvelle transition vers un état différent de
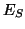 est découverte à partir de
est découverte à partir de  , c'est que la cible
n'existe plus ou qu'elle est accessible à partir d'un autre état.
Nous éliminons alors l'ancienne transition de
, c'est que la cible
n'existe plus ou qu'elle est accessible à partir d'un autre état.
Nous éliminons alors l'ancienne transition de  vers
vers
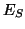 , qui provoque, par réaction, un changement des marquages
du système. S'il n'existe plus de connexion à l'état terminal
, qui provoque, par réaction, un changement des marquages
du système. S'il n'existe plus de connexion à l'état terminal
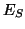 à la suite de la suppression de la transition, nous savons
que l'ensemble des marquages qui étaient strictement positifs
deviendront égaux à 0. S'il existe plusieurs états liés à
à la suite de la suppression de la transition, nous savons
que l'ensemble des marquages qui étaient strictement positifs
deviendront égaux à 0. S'il existe plusieurs états liés à 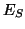 ,
l'ensemble des états appartenant à une politique de commande
empruntant la transition supprimée pourront être modifiés. Deux
cas se présentent pour le marquage associé à un état
,
l'ensemble des états appartenant à une politique de commande
empruntant la transition supprimée pourront être modifiés. Deux
cas se présentent pour le marquage associé à un état  compris dans un chemin passant par la transition supprimée:
compris dans un chemin passant par la transition supprimée:
- il existe un autre chemin entre
 et
et 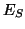 :
dans ce cas, nous savons que le marquage de
:
dans ce cas, nous savons que le marquage de  restera strictement
positif (mais pourra changer de valeur).
restera strictement
positif (mais pourra changer de valeur).
- il n'existe pas d'autre chemin entre
 et
et 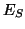 : dans ce
cas, nous savons que le marquage de
: dans ce
cas, nous savons que le marquage de  sera égal à 0.
sera égal à 0.
La prise en compte de la suppression de la cible se fait à
l'instant de la suppression de la transition.




suivant: Découverte de l'ajout d'une
monter: Propriété d'incrémentalité de l'algorithme
précédent: Qu'entendons-nous par ``incrémentalité'' ?
Table des matières
2002-03-01