



suivant: Généralisation du processus de
monter: Perspectives
précédent: Conjecture à propos des
Table des matières
Pour obtenir un algorithme d'AP, il nous faut tout d'abord savoir,
à tout moment, si les contraintes (
 ), CO et CU sont
respectées. Nous avons abordé le problème de CO dans la
sous-section précédente, mais il reste à préciser pour CU. Le
respect de (
), CO et CU sont
respectées. Nous avons abordé le problème de CO dans la
sous-section précédente, mais il reste à préciser pour CU. Le
respect de (
 ) n'est pas difficile à détecter (voir
la méthode de calcul de
) n'est pas difficile à détecter (voir
la méthode de calcul de  et de
et de 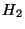 dans la première
partie de ce document). En admettant que le problème de détection
soit résolu, il faut ensuite répondre aux questions suivantes,
dans l'ordre avec lequel elles sont posées:
dans la première
partie de ce document). En admettant que le problème de détection
soit résolu, il faut ensuite répondre aux questions suivantes,
dans l'ordre avec lequel elles sont posées:
- Comment l'environnement agit-il sur la mémoire ?
- Comment la mémoire réagit-elle, si l'action de
l'environnement tend à rompre les contraintes, pour les rétablir ?
- Cette réaction est-elle interprétable comme un apprentissage ?
- Peut-on montrer des propriétés liées à cet apprentissage ?
Le thème central de ces questions est la manière de
modifier la mémoire au fil du temps. Nous pensons à deux
options très différentes. La première consiste à poser une
mémoire vierge (ne contenant aucune hypothèse) à l'instant t=0
et à augmenter progressivement le nombre d'hypothèses au fil de
l'expérience perceptive du système, en sachant que cette augmentation
est modérée par les contraintes CO et CU: nous l'appellerons O1.
La deuxième, notée O2, consiste, au contraire, à considérer, à t=0,
la mémoire la plus grosse possible respectant CO, mais ne respectant
pas théoriquement CU (l'utilisation des mémoires possédant une
infinité d'hypothèses peut être envisagée dans ce cadre). Dans ce
cadre, l'interaction avec l'environnement peut montrer que CU n'est
pas valide (des hypothèses sont associées à plusieurs informations
perceptives), ce qui oblige le système à éliminer des hypothèses
(on pourrait raisonner dans l'espace des paramètres des génératrices
et imaginer l'utilisation du découpage en boîtes de l'algorithme
SIVIA pour rejeter un ensemble de boîtes, donc un ensemble d'hypothèses).
L'option O1 semble peu réaliste si on assimile notre mémoire à la
mémoire biologique, et les hypothèses à un ensemble de neurones.
La seconde est plus plaisante, car elle fait penser au mécanisme de
sélection neuronal, mis en évidence par Edelman ![[*]](file:/usr/lib/latex2html/icons/footnote.png) . Nous préférons, pour cette
raison, ne considérer que O2. Voici notre réflexion menée à partir
de cette option.
. Nous préférons, pour cette
raison, ne considérer que O2. Voici notre réflexion menée à partir
de cette option.
L'idée est de constituer une base initiale d'hypothèses la
plus riche possible (en terme de valeurs de h et de l différentes),
qui respecte l'intégralité des contraintes avant le début de
l'expérience. À notre avis, le terme ``la plus riche possible''
s'interprète par une notion de maximum s'appliquant à la mémoire:
l'ajout d'une hypothèse supplémentaire romprait les contraintes. Nous
notons que la deuxième contrainte de CO ne se pose pas avant le début
de l'expérience, puisque le système n'a pas encore été confronté à des
signaux réels. De même, CU ne se pose pas non plus. La seule condition
porte donc sur la première contrainte de CO. Lorsque le système va
recevoir son premier signal, jamais expérimenté, la première contrainte
de CO va impliquer que le système ne va pas détecter d'information
perceptive, en toute probabilité. Par contre, la deuxième contrainte
de CO va être rompue, puisqu'elle stipule que la détection d'une
information perceptive est assurée en pratique. Comment faire
pour rétablir la deuxième contrainte de CO ? Nous savons, par hypothèse
de construction, qu'on ne peut pas rajouter une nouvelle hypothèse en
mémoire, sous peine de rompre la première contrainte de CO. L'idée est
alors de modifier la génératrice d'un ou de plusieurs focus, de manière
à ce que le signal provoque la détection d'une information perceptive.
Nous souhaiterions que cette modification s'effectue sans changer le
caractère ``maximal'' de la mémoire. Admettons que nous sachions le faire.
Quelles hypothèses faut-il modifier pour assurer cette réaction du système ?
Dans quelle mesure ce changement ne va pas provoquer un ``oubli''
de signaux déjà perçus ? Combien d'hypothèses faut-il modifier ? Imageons
nos propos en utilisant un raisonnement sur les volumes. La première contrainte
de CO impose que le volume de l'ensemble total des vecteurs solutions est
inférieur à un réel 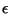 , qui est associé à l'interprétation de la
rareté. Une mémoire de taille maximale est le cas limite pour lequel ce
volume est égal à
, qui est associé à l'interprétation de la
rareté. Une mémoire de taille maximale est le cas limite pour lequel ce
volume est égal à 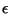 . Le changement de la nature de certains focus
doit s'effectuer à volume constant. En d'autres termes, la modification de
la génératrice de certains focus doit provoquer le déplacement d'une partie
de l'ensemble des vecteurs solutions vers une zone jusque là inoccupée de
l'ensemble des vecteurs solutions. Pour le choix du sous-espace à déplacer,
on pourrait imaginer prendre celui qui a été le moins activé sur une certaine
période de temps. Au bout d'un certain temps, ce mécanisme va permettre de
concentrer le sous-espace des vecteurs solutions théoriques au niveau
du sous-espace des vecteurs solutions pratiques. En d'autres termes,
la deuxième contraintes de CO tendrait à être respectée, alors que la première
le serait toujours.
. Le changement de la nature de certains focus
doit s'effectuer à volume constant. En d'autres termes, la modification de
la génératrice de certains focus doit provoquer le déplacement d'une partie
de l'ensemble des vecteurs solutions vers une zone jusque là inoccupée de
l'ensemble des vecteurs solutions. Pour le choix du sous-espace à déplacer,
on pourrait imaginer prendre celui qui a été le moins activé sur une certaine
période de temps. Au bout d'un certain temps, ce mécanisme va permettre de
concentrer le sous-espace des vecteurs solutions théoriques au niveau
du sous-espace des vecteurs solutions pratiques. En d'autres termes,
la deuxième contraintes de CO tendrait à être respectée, alors que la première
le serait toujours.
Cette réflexion nous semble satisfaisante du point de vue du
respect de CO. Mais, elle n'aborde pas CU.




suivant: Généralisation du processus de
monter: Perspectives
précédent: Conjecture à propos des
Table des matières
2002-03-01