



suivant: Calcul d'un estimateur par
monter: Positionnement de notre démarche
précédent: Valeur des paramètres internes
Table des matières
Éléments de calcul de probabilité
On considère un réel
![$ \epsilon \in ]0,1[$](img65.png) ainsi que la variable aléatoire discrète X, définie par la loi
suivante:
ainsi que la variable aléatoire discrète X, définie par la loi
suivante:
Et P(X=0) = 0
Il s'agit bien d'une loi de probabilité sur
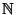 car
car
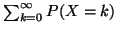 existe et vaut 1.
existe et vaut 1.
L'espérance E[X] se calcule comme suit:
Or, la somme
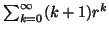 , pour
, pour
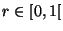 ,
est une somme classique et vaut
,
est une somme classique et vaut
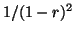 . D'où:
. D'où:
D'autre part, la variance Var[X] est donnée par l'expression suivante:
Nous calculons ![$ E[X^{2}]$](img387.png) :
:
Nous utilisons à nouveau le résultat de la somme classique
suivante:
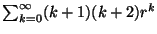 qui vaut
qui vaut
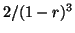 . En décomposant
. En décomposant ![$ E[X^{2}]$](img387.png) pour faire apparaître
cette somme, on obtient:
pour faire apparaître
cette somme, on obtient:
On en déduit l'expression de Var[X]:




suivant: Calcul d'un estimateur par
monter: Positionnement de notre démarche
précédent: Valeur des paramètres internes
Table des matières
2002-03-01
![$\displaystyle E[X] = \sum_{k=0}^{\infty}kP(X=k-1) = \sum_{k=0}^{\infty}(k+1)(1-\epsilon)^{k}$](img381.png)
![$\displaystyle E[X^{2}] = \sum_{k=0}^{\infty}(k+1)^{2}\epsilon(1 - \epsilon)^{k}$](img388.png)