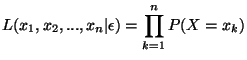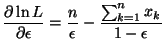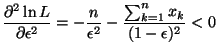suivant: Exemple d'information perceptive pour
monter: Positionnement de notre démarche
précédent: Éléments de calcul de
Table des matières
Calcul d'un estimateur
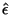 par la méthode du maximum de vraisemblance
par la méthode du maximum de vraisemblance
On considère un réel
![$ \epsilon \in ]0,1[$](img65.png) ainsi que la variable aléatoire discrète X, définie par la
loi suivante:
ainsi que la variable aléatoire discrète X, définie par la
loi suivante:
Et P(X=0) = 0
On considère à présent un n-échantillon
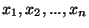 issu de n observations de X. En supposant que ces observations
sont indépendantes, la fonction
issu de n observations de X. En supposant que ces observations
sont indépendantes, la fonction
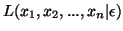 vaut:
vaut:
En prenant le logarithme népérien de L, pour simplifier les calculs, on obtient:
Nous cherchons le maximum de L suivant la variable 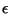 ,
lorsque
,
lorsque
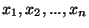 sont fixés. Il vient:
sont fixés. Il vient:
Pour
![$ \epsilon \in ]0,1[$](img65.png) , cette dérivée s'annule pour:
, cette dérivée s'annule pour:
On vérifie que cette valeur correspond bien à un maximum. Pour
cela, il faut regarder la dérivée seconde:
On obtient donc un estimateur
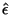 .
Éléments relatifs à la partie II, chapitre 2
.
Éléments relatifs à la partie II, chapitre 2




suivant: Exemple d'information perceptive pour
monter: Positionnement de notre démarche
précédent: Éléments de calcul de
Table des matières
2002-03-01