Définition _s
Dans le cas où les éléments de
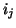
sont tous inférieurs à ceux de
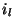
(le signal traverse
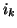
de gauche à droite), nous dirons que
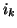
est orienté positivement, ce que nous noterons
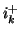
.
Au contraire, dans le cas où les éléments de
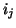
sont tous supérieurs
à ceux de
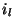
(le signal traverse
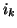
de droite à gauche), nous
dirons que
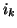
est orienté négativement, ce que nous noterons
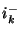
.
![\includegraphics[]{fig/intro_resolution.eps}](img433.png)
![\includegraphics[]{fig/trend.eps}](img439.png)
![\includegraphics[]{fig/signal_incoherent}](img443.png)
![\includegraphics[]{fig/creation_suite.eps}](img444.png)
![\includegraphics[]{fig/coherence_resolution.eps}](img446.png)