



suivant: Preuves concernant la fiabilité
monter: Positionnement de notre démarche
précédent: Découverte de n tendances
Table des matières
Relation entre le paramètre 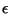 et le postulat
de rareté de l'information perceptive
et le postulat
de rareté de l'information perceptive
Les relations 2.1 et 2.2 (sous-section
2.3.2, page ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) permettent d'établir
une table des triplets (h, i, l) valides, lorsque
) permettent d'établir
une table des triplets (h, i, l) valides, lorsque 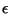 est
fixé. Les valeurs de h, i et l dépendent donc de
est
fixé. Les valeurs de h, i et l dépendent donc de 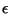 . Quelle
valeur choisir pour ce paramètre ? Pour répondre à cette question, il
faut revenir sur la particularité de notre notion de rareté: un
événement est rare s'il ne se produit pas en pratique, dans la
durée de l'expérience. Nous supposons par là que si la probabilité
pour que l'événement se produise dans la plage de temps de l'expérience
est trop faible, alors cet événement ne se produira pas en réalité. Il
faut donc fixer
. Quelle
valeur choisir pour ce paramètre ? Pour répondre à cette question, il
faut revenir sur la particularité de notre notion de rareté: un
événement est rare s'il ne se produit pas en pratique, dans la
durée de l'expérience. Nous supposons par là que si la probabilité
pour que l'événement se produise dans la plage de temps de l'expérience
est trop faible, alors cet événement ne se produira pas en réalité. Il
faut donc fixer 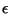 par rapport à la durée de l'expérience ainsi
qu'à un degré de confiance qui sera très proche de 0 en pratique.
par rapport à la durée de l'expérience ainsi
qu'à un degré de confiance qui sera très proche de 0 en pratique.
Le paramètre 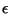 représente la probabilité pour laquelle
une des contraintes de CO ne serait pas respectée. Sa valeur
découle de la tolérance à l'erreur qu'on admet pouvoir supporter
sur une certaine durée D. La probabilité
représente la probabilité pour laquelle
une des contraintes de CO ne serait pas respectée. Sa valeur
découle de la tolérance à l'erreur qu'on admet pouvoir supporter
sur une certaine durée D. La probabilité 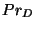 pour qu'aucune
``fausse'' information ne soit générée est donnée par la relation:
pour qu'aucune
``fausse'' information ne soit générée est donnée par la relation:
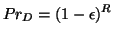 |
(18) |
Avec
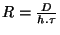 et
et 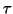 représente la durée moyenne
entre deux appels au processus de catégorisation.
représente la durée moyenne
entre deux appels au processus de catégorisation.
Si on pose
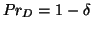 , avec
, avec
![$ \delta \in ]0,1[$](img533.png) , on
en déduit l'expression de
, on
en déduit l'expression de 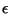 :
:
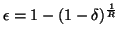 |
(19) |
Si on considère que 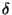 est très inférieur à 1, l'équation
précédente nous donne une forme approchée de
est très inférieur à 1, l'équation
précédente nous donne une forme approchée de 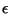 :
:
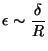 |
(20) |
Pour donner une idée, si on considère un problème pour lequel
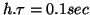 ,
D est égale à une année et
,
D est égale à une année et
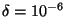 , on trouve
, on trouve
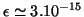 . En revanche, si D vaut 1 sec et
. En revanche, si D vaut 1 sec et
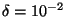 ,
,
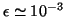 .
.
Les paramètres 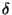 et D dépendent uniquement du contexte
d'application dans lequel on utiliserait le processus de
catégorisation.
et D dépendent uniquement du contexte
d'application dans lequel on utiliserait le processus de
catégorisation.




suivant: Preuves concernant la fiabilité
monter: Positionnement de notre démarche
précédent: Découverte de n tendances
Table des matières
2002-03-01