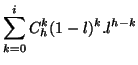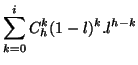suivant: Condition d'existence d'une mémoire
monter: Résolution de CO dans
précédent: Introduction
Table des matières
Notations - Formulation des deux contraintes de CO
L'unique hypothèse est caractérisée par ses trois paramètres:
h, i et l. Dans ce cas, il apparaît que la nature de la génératrice
du focus n'intervient pas dans les calculs de cette section.
Nous supposerons donc que la génératrice est quelconque.
On considère que les h valeurs
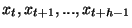 du signal
du signal 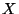 , prises entre les instants t et t+h-1, forment un
h-échantillon issu de variables aléatoires réelles
, prises entre les instants t et t+h-1, forment un
h-échantillon issu de variables aléatoires réelles
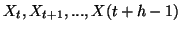 à valeurs dans [0,1], qu'on suppose
indépendantes deux à deux. Nous appellerons ``vecteur solution'' tout
vecteur (
à valeurs dans [0,1], qu'on suppose
indépendantes deux à deux. Nous appellerons ``vecteur solution'' tout
vecteur (
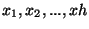 ) respectant les deux contraintes de CO.
L'hypothèse de rareté sera associée à un réel
) respectant les deux contraintes de CO.
L'hypothèse de rareté sera associée à un réel
![$ \epsilon \in ]0,1[$](img65.png)
![[*]](file:/usr/lib/latex2html/icons/footnote.png) .
.
L'expression de la contrainte 1 (voir la sous-section 2.2.4,
page ![[*]](file:/usr/lib/latex2html/icons/crossref.png) )impose que l'événement suivant soit rare: ``Parmi
les h valeurs consécutives d'un signal X quelconque, prises aux instants
t, t+1, ..., t+h-1, il existe au plus i valeurs de X à l'extérieur du
focus associé à l'hypothèse de paramètres h, i et l''.
)impose que l'événement suivant soit rare: ``Parmi
les h valeurs consécutives d'un signal X quelconque, prises aux instants
t, t+1, ..., t+h-1, il existe au plus i valeurs de X à l'extérieur du
focus associé à l'hypothèse de paramètres h, i et l''.
Nommons 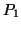 la probabilité que cet événement survienne. L'hypothèse
de rareté impose:
la probabilité que cet événement survienne. L'hypothèse
de rareté impose:
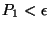 . Voici comment notre problème de
probabilité peut être interprété en terme de calcul de volume de
l'ensemble des solutions vérifiant CO. L'ensemble des valeurs possibles
du vecteur (
. Voici comment notre problème de
probabilité peut être interprété en terme de calcul de volume de
l'ensemble des solutions vérifiant CO. L'ensemble des valeurs possibles
du vecteur (
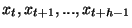 ) est égal à
) est égal à ![$ [0,1]^{h}$](img28.png) ,
de volume 1. La probabilité que nous souhaitons calculer correspond au
rapport entre le volume de l'ensemble des vecteurs solutions (qui est
mesurable) et le volume de l'ensemble des vecteurs possibles. La première
contrainte de CO impose donc que le volume des vecteurs solutions puisse
être inférieur à
,
de volume 1. La probabilité que nous souhaitons calculer correspond au
rapport entre le volume de l'ensemble des vecteurs solutions (qui est
mesurable) et le volume de l'ensemble des vecteurs possibles. La première
contrainte de CO impose donc que le volume des vecteurs solutions puisse
être inférieur à 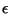 .
.
Dans le cas où i=0, cet ensemble solution est l'hypercube généré par le
focus associé à l'hypothèse. Cet hypercube possède des cotés de longueur l.
On en déduit que son volume est 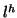 , ce qui correspond à la probabilité
d'occurrence de la détection d'une information perceptive. Dans le cas
général, l'ensemble solution est composé d'un ensemble d'hypercubes
disjoints. Chaque hypercube correspond à l'ensemble des vecteurs
solutions présentant k composantes (
, ce qui correspond à la probabilité
d'occurrence de la détection d'une information perceptive. Dans le cas
général, l'ensemble solution est composé d'un ensemble d'hypercubes
disjoints. Chaque hypercube correspond à l'ensemble des vecteurs
solutions présentant k composantes ( 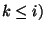 parmi h en dehors de
l'hypercube généré par le focus. Pour k fixé, le volume de tous les
hypercubes est identique et vaut
parmi h en dehors de
l'hypercube généré par le focus. Pour k fixé, le volume de tous les
hypercubes est identique et vaut
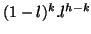 ; le nombre de
ces hypercubes est combinatoire et vaut
; le nombre de
ces hypercubes est combinatoire et vaut 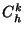 .
.
Les hypercubes étant disjoints deux à deux, on en déduit que le
volume total de l'ensemble des solutions est donné par
l'expression suivante:
La première contrainte de CO impose que ce volume soit inférieur
à 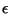 . Elle implique donc que les triplets (h,i,l),
respectant CO vérifient:
. Elle implique donc que les triplets (h,i,l),
respectant CO vérifient:
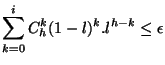 |
(9) |
Cette relation aurait pu être obtenue sans utiliser les volumes,
mais en associant à l'événement élémentaire ``la kième composante
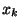 du h-échantillon est incluse dans le focus associée à
l'hypothèse de paramètres h, i et l'' une variable aléatoire discrète
suivant une loi de Bernoulli. On peut alors considérer la variable
aléatoire discrète représentée par la somme de ces h variables aléatoires
supposées indépendantes. Cette nouvelle variable aléatoire suit alors
une loi binomiale de paramètres l et h. La probabilité que nous recherchons
correspond à la probabilité que cette somme soit supérieure ou égale à h-i.
du h-échantillon est incluse dans le focus associée à
l'hypothèse de paramètres h, i et l'' une variable aléatoire discrète
suivant une loi de Bernoulli. On peut alors considérer la variable
aléatoire discrète représentée par la somme de ces h variables aléatoires
supposées indépendantes. Cette nouvelle variable aléatoire suit alors
une loi binomiale de paramètres l et h. La probabilité que nous recherchons
correspond à la probabilité que cette somme soit supérieure ou égale à h-i.
Pour formuler la deuxième contrainte, nous allons considérer que
l'ensemble des signaux perçus réellement peut être modélisé de la
manière suivante. On suppose que l'ensemble des vecteurs
(
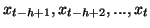 ) sont des réalisations d'un
vecteur Y comportant h variables aléatoires réelles, Y étant mis
sous la forme suivante:
) sont des réalisations d'un
vecteur Y comportant h variables aléatoires réelles, Y étant mis
sous la forme suivante:
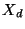 est un vecteur, constant dans le temps, appartenant à
l'hypercube
est un vecteur, constant dans le temps, appartenant à
l'hypercube ![$ [0,1]^{h}$](img28.png) et
et 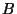 est un vecteur de variables
aléatoires continues
est un vecteur de variables
aléatoires continues
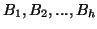 qu'on supposera
indépendantes. Les
qu'on supposera
indépendantes. Les 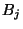 pourront être associées à des lois de
probabilité différentes les unes des autres. Une réalisation de B
sera un vecteur, noté
pourront être associées à des lois de
probabilité différentes les unes des autres. Une réalisation de B
sera un vecteur, noté
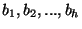 . On considère
également le vecteur (
. On considère
également le vecteur (
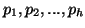 )
)
![$ \in [0,1]^{h}$](img311.png) ,
dont chaque composante
,
dont chaque composante 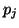 définit la probabilité pour que
définit la probabilité pour que
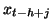 appartienne au focus associé à l'hypothèse de la
mémoire:
appartienne au focus associé à l'hypothèse de la
mémoire:
La seconde contrainte est alors exprimable par la relation suivante:
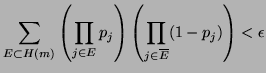 |
(10) |
Avec 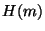 ensemble des parties de
ensemble des parties de
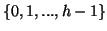 comportant
comportant 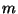 éléments, et
éléments, et
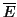 ensembles des
éléments de
ensembles des
éléments de
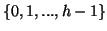 n'appartenant pas à
n'appartenant pas à 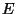 .
.
Cette relation se simplifie dans le cas particulier où les 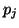 sont tous égaux. On retrouve alors l'expression d'une loi
binomiale, similaire à celle de la relation 2.1.
sont tous égaux. On retrouve alors l'expression d'une loi
binomiale, similaire à celle de la relation 2.1.




suivant: Condition d'existence d'une mémoire
monter: Résolution de CO dans
précédent: Introduction
Table des matières
2002-03-01