Condition d'existence d'une mémoire respectant CO

Nous allons montrer que, sous certaines conditions suffisantes, il est possible de construire une mémoire comportant une hypothèse respectant CO. D'autre part, nous allons montrer que, sous certaines autres conditions suffisantes, aucune mémoire possédant une unique hypothèse ne satisfait CO.
On suppose qu'on connaît précisément la valeur du vecteur $X_{d}$ spécifié dans la sous-section précédente. Dans ce cas, on construit le focus associé à l'hypothèse de la mémoire, de manière à ce que ses valeurs coïncident avec $X_{d}$.
Donnons tout d'abord un exemple, illustrant la proposition qui va suivre (voir la figure 2.2). Dans celui-ci, on suppose que $X_{d}$ est constante dans le temps et vaut 0.5. Nous utiliserons donc un focus dont la génératrice est $X_{d}$ (toutes les composantes du focus sont égales à 0.5). La représentation du focus à un instant t est donnée par le segment horizontal épais d'ordonnée 1, vu dans les graphes (a) et (c). On suppose que les $B_{i}$ suivent toutes la même loi, dont la densité de probabilité diffère suivant les graphes (a), (b) et (c). Les graphes (d), (e) et (f) représentent les visualisations d'une observation du signal dans le temps, issues respectivement des densités de probabilités des graphes (a), (b) et (c). Pour le graphe (b), la courbe de densité de probabilité est confondue avec le segment représentant le focus, qui n'est pas représenté en trait épais. Nous nous intéressons à deux aires différentes:

• l'aire $A_{1}$ délimitée verticalement par le segment représentant le focus (hachurée sur le graphe (a) ), qui représente la probabilité pour qu'une valeur x choisie aléatoirement suivant une loi uniforme sur [0,1] appartienne au focus.
• l'aire $A_{2}$ délimitée par les mêmes points P et Q, concernant la fonction de densité de probabilité. Celle-ci représente les $p_{j}$ (qui sont tous égaux dans ce cas), c'est-à-dire la probabilité pour qu'une valeur x du signal appartienne au focus.

Les trois graphes montrent trois cas:

1. $A_{1} < A_{2}$
2. $A_{1} = A_{2}$
3. $A_{1} > A_{2}$

Nous montrerons que, dans le premier cas, on peut toujours trouver des valeurs de h et i permettant à la fois que le triplet (h,i,l) vérifie CO mais aussi que la détection de l'information perceptive soit fiable: l'exemple typique de loi de probabilité associée aux $B_{i}$ permettant ce cas est la loi normale. On remarque que dans le cas d'une loi normale, n'importe quelle valeur de l nous place dans le cas 1. Le deuxième cas est un cas limite: la densité de probabilité est uniforme sur [0,1]. Dans ce cas, on ne peut pas trouver de triplets (h,i,l). Enfin, le troisième cas est typique de problèmes pour lesquels les données récupérées proviennent de plusieurs sources (deux dans notre exemple). Avec le choix de l du graphe (c), on montre qu'aucun triplet (h,i,l) ne convient; par contre, si on augmente l, on peut (dans notre exemple) retrouver le cas 1, donc trouver des triplets (h,i,l) répondant à nos deux critères (fiabilité de l'information perceptive et respect de CO). Mais, dans ce cas, on ne peut pas séparer les sources. Nous montrerons par la suite qu'il est possible de séparer ces sources en utilisant une mémoire à plusieurs hypothèses, qui pourra être interprétée comme un système de séparation de sources.

Figure: Trois cas de figure, suivant la densité de probabilité associées aux $B_{j}$.

Revenons à notre problématique. Voici ce que nous pouvons montrer dans le cas général:

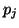
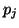
Proposition _s   Pour tout l dans ]0,1[ tel que toutes les probabilités $p_{j}$ sont strictement supérieures à l, alors il existe des valeurs de h et de i telles que (h,i,l) vérifie les deux contraintes associées à CO. D'autre part, pour tout l dans ]0,1[ tel que toutes les probabilités $p_{j}$ sont inférieures ou égales à l, il n'existe pas de valeurs pour h et i telles que (h,i,l) vérifie les deux contraintes de CO à la fois.

Cette proposition signifie que, moyennant certaines conditions suffisantes sur les $p_{j}$, on peut trouver une mémoire possédant une unique hypothèse telle que la détection d'une information perceptive à partir du signal X est fiable . Si on se reporte à l'analogie du processus de catégorisation avec un détecteur de métaux (voir le chapitre précédent), la fiabilité de la détection implique que toute observation $x_{t-h+1},x_{t-h+2},...,x_{t}$ aboutit à la détection d'une information perceptive (celle-ci est unique dans le cas traité par cette section); d'autre part, elle implique qu'aucune détection ne survient, en réalité, à partir d'un vecteur quelconque $y_{1},y_{2},...,y_{h}$. Pour compléter cette proposition, on peut également prouver que l'ensemble des triplets (h,i,l) vérifiant CO et ainsi assurant la fiabilité de la détection de l'information perceptive possèdent une valeur de h minimum strictement supérieure à 1. Cette valeur de h dépend de la valeur du paramètre $\epsilon$ interprétant la notion de rareté.
Nous préférons ne pas donner la preuve de la proposition 7 dans le corps du document de thèse, car elle est longue et ne présente pas d'intérêt pour la compréhension du coeur de notre travail. Le lecteur pourra se reporter à l'annexe B.3, page , pour trouver une démonstration de cette proposition.
La condition suffisante (le cas correspondant à $A_{1} < A_{2}$) permettant d'appliquer le résultat de la proposition 7 est très large. Donnons à présent quelques cas de figure où on peut effectivement obtenir une détection fiable d'information perceptive:

• le signal X est soumis à un bruit gaussien d'amplitude $\sigma$ (exemple du graphe (a) de la figure 2.2, page ). La figure 2.3 montre la relation qui existe entre les paramètre h et l des triplets (h,i,l) valides, lorsque $\sigma$ varie.
• le signal X est soumis a un bruit uniforme d'une amplitude strictement inférieure à 1
• certaines valeurs $x_{t}$ du signal X sont aberrantes (avec un pourcentage de données aberrantes strictement inférieur à 1)

Une détection fiable peut donc être mise en place à partir de signaux de mauvaise qualité, possédant même un taux important de données aberrantes. Le ``prix'' de cette fiabilité est une augmentation de h et/ou de l. Nous verrons par la suite que la contrainte CU imposera alors une diminution du nombre de catégories possibles. Dans le cas où il existe une unique hypothèse, il n'existe donc qu'une catégorie: la contrainte CU n'intervient pas.

Figure: Courbes reliant les paramètres h et l permettant la détection fiable d'un signal de bruit gaussien d'amplitude $\sigma$

Pour cet exemple, la notion de rareté est associée à $\epsilon=10^{-15}$. Les croix indiquent la position du minimum des courbes, relatives à une valeur particulière de $\sigma$.

Admettons qu'on construise la mémoire du système à partir d'un modèle pour lequel $X_{d}$ ne correspond pas tout à fait à la réalité. La fonction génératrice du focus est donc différente de la valeur de $X_{d}$ réel. Cela introduit un biais dans les $B_{j}$ réels, qui n'ont plus une espérance nulle. Lorsque l est fixé, l'augmentation du biais aura tendance à diminuer la valeur des $p_{j}$. Si ce biais est trop élevé (les $p_{j}$ sont tous inférieurs à l), on ne pourra plus garantir la fiabilité de l'information perceptive.
Pour illustrer cela, considérons un ensemble de signaux X dont on sait qu'ils peuvent être modélisés par un $X_{d}$ constant et des $B_{j}$ suivant tous une même loi normale de paramètre $\sigma$. Dans un premier temps, on suppose qu'on possède une valeur approchée de $X_{d}$ et la valeur exacte de $\sigma$ (figure 2.4). On peut déterminer, à partir de $\sigma$, un triplet (h,i,l) permettant d'obtenir une information perceptive fiable (dans le cas où $X_{d}$ est connu exactement). Nous allons étudier l'influence de l'imprécision de $X_{d}$ sur le taux de détection d'une information perceptive.

Figure: Imprécision sur $X_{d}$.

L'écart entre $X_{d}$ théorique (égal à 0.5) et $X_{d}$ réel est matérialisé par la distance entre les deux lignes en pointillés.

Pour cela, lorsque $X_{d}$ réel est fixé, nous soumettons le système de catégorisation au signal X, avec $X_{d}$ réel = 0.5 et $\sigma$ = 0.05, pendant 10.000 pas de temps et nous comptons le nombre d'informations perceptives reçues . La figure 2.5 montre les résultats. On constate que le taux de détection de l'information perceptive est maximum jusqu'à une certaine valeur de l'écart entre $X_d$ réel et $X_{d}$ estimé. Au delà de ce seuil, la performance chute brusquement. La valeur de ce seuil dépend du paramètre l. Lorsque l'écart grandit beaucoup, le taux de détection tend vers 0. Ce résultat n'est pas surprenant. L'information la plus intéressante est la nature des courbes obtenues: elles sont formées de deux plateaux, l'un contenant des valeurs de l'écart associées à un taux de détection maximal, l'autre contenant des valeurs de l'écart associées à un taux de détection nul. La largeur du premier plateau indique l'ensemble des focus associés à la même hypothèse (h,i,l) permettant une détection fiable de l'information perceptive pour le signal X. On peut effectuer une expérience similaire, mais en considérant une imprécision sur la valeur de $\sigma$. Les résultats sont donnés par la figure 2.6. Ils sont semblables à ceux trouvés ci-dessus.

Figure: Évolution du taux de détection de l'information perceptive en fonction de l'imprécision sur $X_{d}$

La mémoire est construite de manière à permettre la fiabilité de l'information perceptive pour un signal aléatoire gaussien X, de paramètre $\sigma=0.05$. La notion de fiabilité est associée à une valeur de $\epsilon=10^{-15}$.

Figure: Évolution du taux de détection de l'information perceptive en fonction de l'imprécision sur $\sigma$

La mémoire est construite de manière à permettre la fiabilité de l'information perceptive pour un signal aléatoire gaussien X, de paramètre $\sigma=0.05$. La notion de fiabilité est associée à une valeur de $\epsilon=10^{-15}$.