Contrainte d'observabilité CO, restreignant l'information perceptive - Lien avec l'AP

La contrainte CO est, en fait, composée de deux contraintes antagonistes appliquées sur la mémoire, que nous allons spécifier.

1. Une condition nécessaire, pour que la sortie du processus de catégorisation soit une information perceptive, est que les caractéristiques de la mémoire en entrée de ce dernier permettent de garantir que la production d'une sortie S(t) par le mécanisme de sélection est un événement théoriquement rare
2. Une autre condition nécessaire est que la non production d'une sortie S(t) soit un événement rare en pratique

Il faut expliquer la différence entre les deux termes ``théorique'' et ``pratique''. Dans le premier cas, on considère qu'un signal X quelconque, mis à l'entrée du processus de catégorisation, n'aboutit que rarement à la détection d'une information perceptive. En d'autres termes, l'ensemble des signaux aboutissant à une sortie S(t) est beaucoup plus petit que l'ensemble total des signaux. Il faut rapprocher cette restriction de notre volonté d'éviter, avec une forte probabilité, une fausse détection d'un problème de catégorie 2, dans le problème ``D''. Nous assimilons donc le problème consistant à anticiper l'évolution d'un signal quelconque à un problème de catégorie 1, ce qui semble réaliste. Au contraire, dans le second cas, on considère qu'un signal X, expérimenté en réalité par le système, aboutit presque toujours à la détection d'une information perceptive. Cela signifie que la mémoire du système est construite de manière à ce que le mécanisme de sélection aboutisse, presque sûrement, à une sortie S(t) non vide: cela est en relation avec le fait de détecter, d'une manière fiable, un problème de catégorie 2 dans le problème ``D''.
Il faut noter que notre raisonnement est fondé sur l'hypothèse (pragmatique) que l'ensemble des signaux (évoluant dans le temps) auxquels le système fera réellement face est bien plus petit que l'ensemble des signaux imaginables. Nous nous inspirons donc du cas des lymphocytes T, donné dans notre avant-propos, pour lequel le même constat d'échec peut être effectué si l'ensemble des ennemis réellement rencontrés est trop gros.
Nous voyons le rôle central de la mémoire, donc du choix des hypothèses d'évolution: elle doit être construite de manière à respecter la double exigence suivante:

• l'ensemble des hypothèses ne doit pas être trop gros par rapport à l'ensemble total des hypothèses imaginables (contrainte 1)
• l'ensemble des hypothèses doit permettre de dégager une information perceptive pour tout signal qui est mis réellement en entrée du système (contrainte 2)

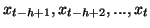Dans notre modélisation, lorsque h est fixé, l'ensemble des signaux imaginables, qui ont tous des valeurs dans [0,1] par hypothèse, est isomorphe à $[0,1]^{h}$ . La contrainte 1 s'exprime en calculant le volume de l'ensemble des vecteurs ( $x_{t-h+1},x_{t-h+2},...,x_{t}$) mis en entrée du processus de catégorisation, produisant un ensemble S(t) non vide. La contrainte de rareté s'applique sur la mémoire de manière à ce que ce volume soit très petit par rapport au volume de l'ensemble des signaux imaginables. Il faut noter que cette contrainte est indépendante de la nature des signaux en entrée du système: elle est inhérente à la mémoire.
La deuxième contrainte est liée à une bonne adéquation entre la mémoire et les vecteurs ( 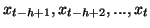$x_{t-h+1},x_{t-h+2},...,x_{t}$) qui vont être utilisés réellement par le processus de catégorisation. Celle-ci tient compte de l'interaction, pendant l'expérience, entre le système et son environnement .
Dans l'optique d'une émergence de l'apprentissage perceptif, on peut considérer que la double contrainte CO, appliquée à la mémoire, doit être validée à chaque pas de temps . D'après notre méthodologie, une rupture de ces contraintes doit aboutir à une modification de la mémoire pour rétablir la contrainte CO. Or, dans quels cas cette contrainte est-elle rompue ? Premièrement, si un signal présenté à l'entrée du système n'aboutit à aucune information perceptive (rupture de la deuxième contrainte). Deuxièmement, si la mémoire ne satisfait plus au critère de rareté théorique de l'information perceptive (rupture de la première contrainte). Un algorithme d'AP doit permettre cette transformation de la mémoire: cette transformation correspondra à un apprentissage.
Mais, avant de pouvoir déterminer un algorithme d'AP, il faut d'abord pouvoir vérifier le respect de CO (contrainte d'équilibre). Nous montrerons dans des cas simples que la contrainte de rareté théorique de l'information perceptive pose un problème de probabilité (voir la section2.3). Toutefois, nous n'avons pas résolu ce problème de probabilité dans le cas général: il s'agit, pour le moment, d'un problème en cours d'étude.