Extensions du problème ``D''

Les problèmes utilisant la perception n'appartiennent jamais à une des deux catégories citées dans le problème ``D'': il existe toujours une part d'aléas. Voici comment nous pouvons étendre la définition de la catégorie 2 pour obtenir un résultat similaire à celui du problème ``D'' dans les cas où aucun problème posé au cobaye n'est totalement déterministe. Il suffit, pour cela, de donner au cobaye la possibilité de se tromper sur un certain nombre de réponses parmi les h possibles: c'est la signification du paramètre i. On sent bien que les problèmes de catégorie 1 ne seront jamais résolus si h est assez grand et i raisonnablement petit (par rapport à h). Nous utilisons alors notre raisonnement inductif pour décréter que, si la probabilité que le cobaye donne une bonne réponse au hasard (malgré les i erreurs qui lui sont accordées) est très faible, et que ce dernier donne néanmoins au moins h-i bonnes réponses, alors c'est un problème de catégorie 2 qui est traité.
Nous pouvons encore donner plus de chances à notre cobaye: nous allons l'autoriser non seulement à commettre au plus i erreurs mais également à donner plusieurs grilles de réponses (chacune comportant h réponses). Pour chacune d'entre-elles, i erreurs sont tolérées. Cet ensemble de réponses possible pourra être comparé à l'existence de plusieurs hypothèses au sein de la mémoire en entrée du processus de catégorisation.
Mais nous voyons apparaître un problème: reprenons le cas du jet de pièce, qui est de catégorie 1. Admettons que le cobaye doive prévoir la succession des pile et face sur 100 jets, avec aucune possibilité d'erreur sur les 100 jets (i=0). Que se passe-t-il si on ne restreint pas le nombre de grilles que le cobaye peut remplir ? Il pourra en livrer 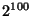$2^{100}$, comportant chacune une combinaison différente, ce qui lui permettra de trouver la bonne réponse à coup sûr. L'observateur en déduira à tort que le problème du cobaye est de catégorie 2. Il est donc nécessaire de limiter le nombre d'hypothèses possibles, de manière à conserver la possibilité d'avoir une probabilité de bonne réponse très faible. Le raisonnement inductif peut alors s'appliquer pour détecter un problème de catégorie 2.
Par conséquent, les paramètres qui influent sur la fiabilité de la décision de l'observateur (ou du processus de catégorisation) sont les composantes de la mémoire en entrée de ce processus: les paramètres h, i et l (l est en rapport avec la probabilité pour que le cobaye donne une unique bonne réponse au hasard: il vaudrait 1/2 dans le cas des deux exemples du problème ``D'') ainsi que le nombre et la nature des hypothèses sont déterminants.