



suivant: Extensions du problème ``D''
monter: Contraintes associées à l'information
précédent: Introduction
Table des matières
Nous souhaitons expliquer l'importance du paramètre h de la mémoire
du système. Ce paramètre influe sur la dimensionnalité théorique de
l'ensemble des signaux possibles: Un signal pris entre les instants
t et t+h permet d'engendrer un vecteur de dimension h (en normalisant
le pas d'échantillonnage à 1). L'idée est que l'information perceptive
découverte est fiable uniquement si la probabilité de découverte au
hasard d'une telle information est très faible. Dans ces conditions,
le guide permettant de découvrir l'information perceptive est l'expérience
du système, emmagasinée dans sa mémoire. Nous illustrons cela par l'exemple
nommé problème ``D'' ![[*]](file:/usr/lib/latex2html/icons/footnote.png) . Celui-ci va expliciter
la caractéristique de rareté de l'information perceptive et son lien avec
la mémoire. Il met en scène une personne cobaye, qui doit donner des réponses
à des questions posées, et un observateur qui ne connaît pas la nature du
problème, mais sait si la personne cobaye a bien répondu ou non. C'est
l'observateur qui nous intéresse: il doit décider, à partir des résultats
de la personne cobaye, si celle-ci a répondu au hasard ou en utilisant
ses connaissances sur le problème posé.
. Celui-ci va expliciter
la caractéristique de rareté de l'information perceptive et son lien avec
la mémoire. Il met en scène une personne cobaye, qui doit donner des réponses
à des questions posées, et un observateur qui ne connaît pas la nature du
problème, mais sait si la personne cobaye a bien répondu ou non. C'est
l'observateur qui nous intéresse: il doit décider, à partir des résultats
de la personne cobaye, si celle-ci a répondu au hasard ou en utilisant
ses connaissances sur le problème posé.
Voici l'énoncé du problème ``D''.
Considérons les deux classes de problèmes suivantes:
- Imaginons que nous jetions une pièce de monnaie en l'air à l'instant t.
Considérons l'ensemble des événements possibles générés par ce jet
à l'instant t+1: ``la pièce tombe sur pile'' et la ``pièce tombe
sur face''. A priori, si la pièce est correctement
équilibrée, ces deux événements sont statistiquement aussi
probables l'un que l'autre. Imaginons à présent une personne
jetant cette pièce à l'instant t, après avoir effectué une
prévision sur le résultat du jet, à l'instant t-1. D'un point de
vue statistique, le taux de bonnes prédictions sur un nombre
d'essais très grand correspond à la probabilité objective que la
pièce tombe sur pile ou sur face. Ainsi, si la personne effectue
non pas un jet mais disons 100 jets, après avoir donné une
prédiction sur l'enchaînement précis des 100 jets, la probabilité
de justesse de l'intégralité de la prédiction est égale à
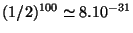 . Cette très faible probabilité
de deviner la bonne réponse est due à la très grande dimension de
l'univers des possibilités qui sont offertes à la personne lors de
son choix (dans notre exemple, il y en a exactement
. Cette très faible probabilité
de deviner la bonne réponse est due à la très grande dimension de
l'univers des possibilités qui sont offertes à la personne lors de
son choix (dans notre exemple, il y en a exactement
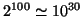 ). D'autre part, il paraît raisonnable d'affirmer
que la personne servant de cobaye à l'expérience n'influence pas
le résultat de celle-ci. Sachant cela, que penserions-nous si
cette personne avait effectivement deviné l'enchaînement exact des
jets, malgré cette si faible probabilité de bonne réponse ?
). D'autre part, il paraît raisonnable d'affirmer
que la personne servant de cobaye à l'expérience n'influence pas
le résultat de celle-ci. Sachant cela, que penserions-nous si
cette personne avait effectivement deviné l'enchaînement exact des
jets, malgré cette si faible probabilité de bonne réponse ?
- Considérons à présent une personne devant répondre à un
questionnaire comportant 100 questions. Admettons que celle-ci ait
deux possibilités de réponses: ``vrai'' ou ``faux'' et que les
questions soient toutes du type ``Le nombre entier 'n' est pair''.
Pour déterminer les 100 entiers du questionnaire, on les choisit
entièrement au hasard, en imposant simplement qu'un entier ne soit
choisi qu'une fois au plus. Si on considère la personne comme un
acteur passif de l'expérience
![[*]](file:/usr/lib/latex2html/icons/footnote.png) , la probabilité objective pour que
les réponses au questionnaire soient toutes exactes est la même
que celle de l'expérience précédente, puisqu'il existe une chance
sur deux de répondre correctement à chaque question.
, la probabilité objective pour que
les réponses au questionnaire soient toutes exactes est la même
que celle de l'expérience précédente, puisqu'il existe une chance
sur deux de répondre correctement à chaque question.
Les deux expériences sont objectivement similaires et possèdent deux
univers des possibilités de même dimension. Pourtant, un élément
essentiel diffère: dans le premier cas, on peut raisonnablement
supposer que la personne cobaye ne maîtrise pas le résultat de son
jet, donc que ses prévisions sont purement spéculatives, alors que
dans le second cas, si la personne cobaye possède la notion de nombre
pair ou impair, elle saura répondre avec certitude à l'intégralité du
questionnaire. Mais comment discerner en pratique ces deux cas de
figures ? Pour cela, admettons qu'une deuxième personne (l'observateur)
puisse choisir a priori l'étendue de l'univers des possibilités
offertes à la personne cobaye, commun aux deux expériences, sans pour
autant en connaître la nature: elle est avertie uniquement de la qualité
des résultats de la personne cobaye pour chacune des deux tâches, sans
savoir en quoi celles-ci consistent, mais en maîtrisant toutefois la
probabilité de bonne réponse. Dans notre exemple, cela signifie que
l'observateur donne a priori le nombre de jets, ainsi que le
nombre de questions (qui sont identiques dans ce cas précis). Une
technique simple permettant de discerner les deux expériences est de
regarder l'évolution des bonnes réponses en fonction d'une augmentation
progressive de la taille de l'univers des possibilités. On imagine
facilement que, pour la première expérience, une demande de prévision
sur l'enchaînement d'un nombre de jets trop important n'aboutira à
aucune bonne réponse. En ce qui concerne la deuxième expérience, le même
résultat sera obtenu si la personne cobaye ne connaît pas la notion de
nombre pair, alors qu'un résultat invariablement positif sera obtenu dans
le cas contraire, quel que soit le nombre des questions. Nous souhaitons
fixer h de manière à ce que les problèmes de catégorie 1 ne puissent être
résolus que rarement. Ainsi, lorsque h augmente, le taux de bonnes
réponses du cobaye diminue pour les problèmes de catégorie 1 mais reste
très bon pour les problèmes de catégorie 2. Si on considère un observateur
ne connaissant pas le problème du cobaye, mais décidant du nombre h,
celui-ci peut déterminer, simplement en faisant augmenter h, quelle est
la catégorie du problème que traite le cobaye. Il faut bien noter que cette
réponse est dépendante des capacités du cobaye, si celui-ci est confronté
à un problème de catégorie 2 qu'il ne sait pas résoudre: en effet, le cobaye
donnerait alors des réponses aléatoires, comme s'il avait été confronté à
un problème de catégorie 1.
Ainsi, si on augmente suffisamment la valeur de h, nous savons que la
probabilité pour que le cobaye trouve une bonne réponse pour un problème
de catégorie 1 est très faible (cet événement est rare). Nous utilisons
alors un raisonnement inductif pour supposer que, si la personne
cobaye donne une bonne réponse alors que h est suffisamment élevé,
cela signifie que le problème ne peut pas être de catégorie 1. Dans ce
cas, une unique bonne réponse suffit pour dire que le problème
est de catégorie 2.
Voici comment nous pouvons interpréter le problème ``D''.
L'observateur est le processus de catégorisation. Le choix du
cobaye est assimilable à une hypothèse contenue dans la
mémoire en entrée du processus de catégorisation. Dans notre cas,
h vaudrait 100 et on souhaiterait qu'il y ait une bonne réponse
sur l'intégralité des questions, ce qui signifie que i vaudrait 0
(aucune erreur admise). Enfin, un seul choix est proposé au
cobaye, ce qui peut être interprété par le fait que la mémoire en
entrée du processus de catégorisation est composée d'une unique
hypothèse.




suivant: Extensions du problème ``D''
monter: Contraintes associées à l'information
précédent: Introduction
Table des matières
2002-03-01