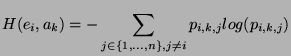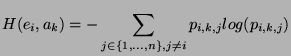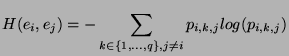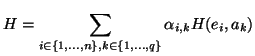suivant: Protocole de calcul des
monter: Outils d'étude de l'incertitude
précédent: Information associée à l'exécution
Table des matières
Nous allons nous intéresser à l'information qui peut être
dégagée de l'exécution d'une action 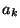 . Intuitivement, on
peut relier le fait que
. Intuitivement, on
peut relier le fait que 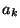 agit sur le système avec le changement
d'état du système. Dans le cas général, ce changement d'état est
soumis à l'incertitude, dans le sens où si on connaît parfaitement
agit sur le système avec le changement
d'état du système. Dans le cas général, ce changement d'état est
soumis à l'incertitude, dans le sens où si on connaît parfaitement
 et
et 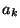 , il se peut qu'on puisse ne pas prédire avec
certitude la nature de l'état
, il se peut qu'on puisse ne pas prédire avec
certitude la nature de l'état 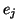 obtenu à l'instant t+h. C'est
le sens des probabilités
obtenu à l'instant t+h. C'est
le sens des probabilités 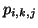 lorsque i et k sont fixés. De même,
si on connaît parfaitement deux états par lequel le système est passé
consécutivement, on peut ne pas déduire quelle action
lorsque i et k sont fixés. De même,
si on connaît parfaitement deux états par lequel le système est passé
consécutivement, on peut ne pas déduire quelle action 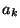 a permis
le passage d'un état à l'autre: c'est le sens des probabilités
a permis
le passage d'un état à l'autre: c'est le sens des probabilités 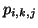 lorsque i et j sont fixés.
lorsque i et j sont fixés.
Par conséquent, nous avons deux mesures différentes, dont
l'objectif est de donner une idée de l'incertitude associée soit à
la prédiction de l'état futur, soit à la déduction de l'action
exécutée par le système. L'utilisation de l'entropie semble donc
adaptée à notre problématique. Pour un état  et une action
et une action
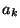 fixés, nous définissons l'entropie
fixés, nous définissons l'entropie
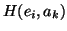 associée à l'incertitude sur l'état suivant comme suit:
associée à l'incertitude sur l'état suivant comme suit:
De même, pour un état  et un état
et un état 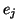 , nous spécifions
l'entropie
, nous spécifions
l'entropie
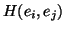 associée à l'incertitude sur l'action
qui a permis le passage de l'état
associée à l'incertitude sur l'action
qui a permis le passage de l'état  à l'état
à l'état 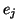 .
.
L'étude détaillée de la fonction H a été effectuée pour la première
fois par Shannon dans le cadre de la théorie de l'information
[Shannon, 1948]. À partir de cette étude, nous savons que
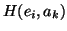 est minimale et vaut 0 dans le cas où un unique
est minimale et vaut 0 dans le cas où un unique
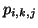 est non nul et vaut 1 (prédictibilité parfaite du
résultat de l'action
est non nul et vaut 1 (prédictibilité parfaite du
résultat de l'action 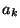 ). À l'autre extrême,
). À l'autre extrême,
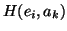 est maximale lorsque les
est maximale lorsque les 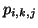 sont tous égaux (incertitude
maximale sur le résultat de l'action
sont tous égaux (incertitude
maximale sur le résultat de l'action 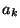 ). De même,
). De même,
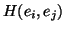 est minimale et vaut 0 lorsqu'il existe une action permettant de passer
de l'état
est minimale et vaut 0 lorsqu'il existe une action permettant de passer
de l'état  à l'état
à l'état 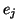 . Au contraire,
. Au contraire,
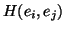 est
maximale lorsque touts les actions ont une probabilité égale d'avoir
permis le passage de l'état
est
maximale lorsque touts les actions ont une probabilité égale d'avoir
permis le passage de l'état  à l'état
à l'état 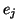 .
.
On remarque que
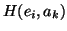 est minimale et nulle lorsque
l'action
est minimale et nulle lorsque
l'action 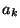 est parfaitement discriminante à partir de l'état
est parfaitement discriminante à partir de l'état
 : l'ensemble des probabilités
: l'ensemble des probabilités 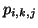 sont nulles sauf une
qui vaut 1 (lorsque i et k sont fixés). De même,
sont nulles sauf une
qui vaut 1 (lorsque i et k sont fixés). De même,
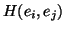 est
minimale lorsque les états sont parfaitement discriminants par rapport
aux actions. Lorsque ces deux cas sont réunis, l'état
est
minimale lorsque les états sont parfaitement discriminants par rapport
aux actions. Lorsque ces deux cas sont réunis, l'état  vérifie
la propriété (P).
vérifie
la propriété (P).
À partir des définitions de
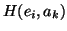 et de
et de
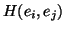 pour un état particulier
pour un état particulier  , peut-on
mesurer le caractère informatif du système total (incluant tous
les états et toutes les actions possibles) ? Avant de répondre à
cette question, trois contraintes existent:
, peut-on
mesurer le caractère informatif du système total (incluant tous
les états et toutes les actions possibles) ? Avant de répondre à
cette question, trois contraintes existent:
- la mesure sur le système total doit être minimale lorsque le
contexte de l'apprentissage vérifie la propriété (P)
- la mesure sur le système total ne doit tenir compte que des états
qui sont effectivement explorés
- la mesure du système total ne doit pas être influencée par
l'apprentissage
À partir de la première contrainte, l'expression générale de la
mesure de la qualité de discrimination des actions est la
suivante:
avec:
et
La dernière contrainte signifie qu'on souhaite pouvoir mesurer la
qualité du contexte de l'apprentissage seul. Il ne faut donc pas
utiliser l'estimation des 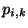 pour pondérer les
pour pondérer les
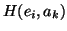 ,
car ces valeurs dépendent de la politique de commande du système
(certains états ne seront quasiment jamais visités, alors que
d'autres le seront fréquemment).
,
car ces valeurs dépendent de la politique de commande du système
(certains états ne seront quasiment jamais visités, alors que
d'autres le seront fréquemment).
Une mesure  peut être envisagée en donnant autant de poids
à chaque
peut être envisagée en donnant autant de poids
à chaque
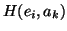 : on aura
: on aura
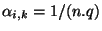 . Il
vient:
. Il
vient:
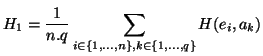 |
(1) |
Pour répondre à l'exigence de la deuxième contrainte, on pourra
modifier le facteur n.q de manière à ne compter que les états
 effectivement atteints.
Une mesure
effectivement atteints.
Une mesure 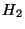 est obtenue pareillement, avec
est obtenue pareillement, avec
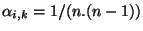 :
:
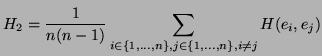 |
(2) |




suivant: Protocole de calcul des
monter: Outils d'étude de l'incertitude
précédent: Information associée à l'exécution
Table des matières
2002-03-01