Les états perceptifs  sont représentés par des cercles, alors
que les états transitoires sont représentés par des cercles, alors
que les états transitoires  sont représentés par des carrés.
Dans cet exemple, le système possède trois actions. À l'instant t, le
système est dans l'état sont représentés par des carrés.
Dans cet exemple, le système possède trois actions. À l'instant t, le
système est dans l'état 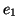 , qui est lié à trois états transitoires
(dépendant du choix entre trois actions possibles). Les transitions (en pointillé)
sont le résultat des expériences passées du système, liant l'exécution de chacune
de ces actions à un certain nombre d'états perceptifs. , qui est lié à trois états transitoires
(dépendant du choix entre trois actions possibles). Les transitions (en pointillé)
sont le résultat des expériences passées du système, liant l'exécution de chacune
de ces actions à un certain nombre d'états perceptifs.
La propriété (
 ) se traduit sur ce graphe par
l'existence, en pratique, d'une unique transition entre un état
transitoire et un état perceptif. ) se traduit sur ce graphe par
l'existence, en pratique, d'une unique transition entre un état
transitoire et un état perceptif. |
![\includegraphics[]{fig/graphe2.eps}](img133.png)
![\includegraphics[]{fig/graphe2.eps}](img133.png)