



suivant: Problème du labyrinthe
monter: Propriété d'incrémentalité de l'algorithme
précédent: Découverte de l'ajout d'un
Table des matières
Pour obtenir le caractère d'incrémentalité de l'algorithme
CbL(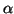 ), il nous faut supposer que le contexte de
l'apprentissage respecte la propriété (
), il nous faut supposer que le contexte de
l'apprentissage respecte la propriété (
 ). En effet,
nous nous basons sur ce postulat pour discerner une modification de
l'environnement (cas où une deuxième transition doit être créée à
partir d'un état
). En effet,
nous nous basons sur ce postulat pour discerner une modification de
l'environnement (cas où une deuxième transition doit être créée à
partir d'un état  ).
).
La propriété (
 ) peut être vue comme un invariant
structurel du graphe, à l'instar de la contrainte d'équilibre
reliant les marquages d'états voisins. Si on considère que cette
propriété doit être respectée à chaque pas de temps, la tentative
de création d'une deuxième transition à partir d'un état
) peut être vue comme un invariant
structurel du graphe, à l'instar de la contrainte d'équilibre
reliant les marquages d'états voisins. Si on considère que cette
propriété doit être respectée à chaque pas de temps, la tentative
de création d'une deuxième transition à partir d'un état  invalide cet invariant. Pour le rétablir, il suffit de supprimer
l'ancienne transition. La modification de l'environnement est alors
perçue par le système comme une double opération d'ajout et de
suppression de transitions à partir d'un même état
invalide cet invariant. Pour le rétablir, il suffit de supprimer
l'ancienne transition. La modification de l'environnement est alors
perçue par le système comme une double opération d'ajout et de
suppression de transitions à partir d'un même état  .
L'observation de ce changement à travers le graphe d'états est
alors une propriété émergente de l'invariant structurel sous-jacent
à la propriété (
.
L'observation de ce changement à travers le graphe d'états est
alors une propriété émergente de l'invariant structurel sous-jacent
à la propriété (
 ).
).
Ce changement mineur de l'algorithme CbL est effectuée simplement,
en modifiant légèrement l'algorithme 2.2, page
![[*]](file:/usr/lib/latex2html/icons/crossref.png) : au niveau de la création d'une transition, il
suffit de regarder si une autre transition partant de
: au niveau de la création d'une transition, il
suffit de regarder si une autre transition partant de  existe déjà et la supprimer le cas échéant. Dans le cas d'une
suppression, il faut appeler l'algorithme 2.1,
page
existe déjà et la supprimer le cas échéant. Dans le cas d'une
suppression, il faut appeler l'algorithme 2.1,
page ![[*]](file:/usr/lib/latex2html/icons/crossref.png) , pour une mise en cohérence des
marquages. La politique de commande est alors modifiée
naturellement par l'ajout ou la suppression d'une cible
(c'est-à-dire par la découverte d'une nouvelle transition vers
, pour une mise en cohérence des
marquages. La politique de commande est alors modifiée
naturellement par l'ajout ou la suppression d'une cible
(c'est-à-dire par la découverte d'une nouvelle transition vers
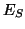 ), ainsi que par l'ajout d'une source d'erreurs
(c'est-à-dire par la découverte d'une nouvelle transition vers
), ainsi que par l'ajout d'une source d'erreurs
(c'est-à-dire par la découverte d'une nouvelle transition vers
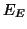 ). La prise en compte de la suppression d'une source
d'erreurs n'est intéressante que dans le cas où le système est
confiné dans un ensemble restreint d'états viables sans pouvoir
atteindre l'objectif. Dans ce cas, il est nécessaire d'ajouter une
stratégie de haut niveau, commandant régulièrement la suppression
des transitions vers
). La prise en compte de la suppression d'une source
d'erreurs n'est intéressante que dans le cas où le système est
confiné dans un ensemble restreint d'états viables sans pouvoir
atteindre l'objectif. Dans ce cas, il est nécessaire d'ajouter une
stratégie de haut niveau, commandant régulièrement la suppression
des transitions vers 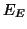 , afin de permettre une nouvelle phase
d'exploration, permettant si possible de trouver un chemin vers
l'objectif.
, afin de permettre une nouvelle phase
d'exploration, permettant si possible de trouver un chemin vers
l'objectif.




suivant: Problème du labyrinthe
monter: Propriété d'incrémentalité de l'algorithme
précédent: Découverte de l'ajout d'un
Table des matières
2002-03-01