La figure de gauche montre des états 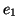 , , 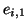 et et
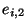 dont les marquages sont cohérents. L'ajout d'une
transition entre dont les marquages sont cohérents. L'ajout d'une
transition entre 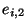 et et 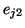 rompt cette cohérence,
puisque le marquage de rompt cette cohérence,
puisque le marquage de 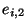 vaut 0 et n'est plus égal au
minimum des marquages associés aux états voisins ( vaut 0 et n'est plus égal au
minimum des marquages associés aux états voisins (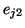 ). La
figure de gauche montre le graphe après le rétablissement de la
cohérence entre les marquages. On note que la valeur de ). La
figure de gauche montre le graphe après le rétablissement de la
cohérence entre les marquages. On note que la valeur de  a
également été modifiée. Ce changement pourrait, à son tour,
provoquer un changement des marquages associés aux états connectés
à a
également été modifiée. Ce changement pourrait, à son tour,
provoquer un changement des marquages associés aux états connectés
à  , qui n'apparaissent pas sur le schéma. , qui n'apparaissent pas sur le schéma. |
![\includegraphics[]{fig/ajout_trans.eps}](img147.png)
![\includegraphics[]{fig/ajout_trans.eps}](img147.png)

