suivant: Algorithme d'apprentissage CbL
monter: Description de l'algorithme CbL
précédent: Marquage des états du
Table des matières
Contraintes du système subissant l'AO
Le problème lié au marquage des états provient de l'ignorance
a priori de l'effet des actions sur le passage d'un état à
l'autre (on suppose qu'on ne possède pas de modèle de la dynamique
du problème). Nous allons considérer que, dans ce cadre, le choix de
l'action peut être vu comme un problème de prise de décision associé à
un jeu à deux joueurs: un joueur serait le système (qui possède, à chaque
pas de temps, q coups possibles), alors que l'autre joueur serait la
dynamique du système. À chaque instant, l'objectif du système est
d'empêcher son adversaire (la dynamique) de le pousser vers l'état
terminal, ce qui signifierait la perte de la partie (échec du respect
des contraintes).
La propriété (
 ) nous indique que l'adversaire ne peut
utiliser qu'un coup, avec une probabilité proche de 1. Mais, la nature
de ce coup est inconnue a priori: c'est l'expérience qui la précise.
) nous indique que l'adversaire ne peut
utiliser qu'un coup, avec une probabilité proche de 1. Mais, la nature
de ce coup est inconnue a priori: c'est l'expérience qui la précise.
Nous nous inspirons de l'algorithme minimax [Rich, 1983], dans
le but de déterminer la valeur des marquages associés à chaque
état. Voici l'énoncé de la contrainte d'équilibre, valable pour
chaque état, à chaque pas de temps. Celle-ci précise la valeur du
marquage  de chaque état perceptif
de chaque état perceptif  ainsi que le
marquage
ainsi que le
marquage  de chaque état transitoire
de chaque état transitoire  , en
fonction du marquage des états connectés à ces derniers:
, en
fonction du marquage des états connectés à ces derniers:
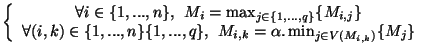 |
(6) |
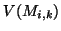 est l'ensemble des indices des états perceptifs vers
lesquels une transition issue de l'état transitoire
est l'ensemble des indices des états perceptifs vers
lesquels une transition issue de l'état transitoire  aboutit. On supposera que si
aboutit. On supposera que si
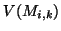 est vide, alors
est vide, alors
 vaut 0. Cette supposition est importante pour que
l'ensemble des marquages initiaux soient cohérents (voir la
sous-section 2.2.5). Dans le cas où
vaut 0. Cette supposition est importante pour que
l'ensemble des marquages initiaux soient cohérents (voir la
sous-section 2.2.5). Dans le cas où
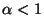 ,
,
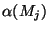 vaut 1 lorsque
vaut 1 lorsque 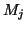 est égal à -1 ou 0, est
égal à
est égal à -1 ou 0, est
égal à
![$ \alpha \in ]0,1]$](img137.png) si
si
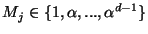 et est égal à 0 si
et est égal à 0 si
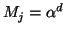 . Dans le
cas particulier où
. Dans le
cas particulier où
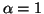 , on fixera
, on fixera
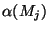 à 1,
quel que soit
à 1,
quel que soit 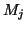 . La contrainte appliquée au graphe d'états
lie les valeurs des marquages associés à des états voisins (reliés
par une transition). Nous verrons qu'il existe une différence
entre les algorithmes Cb1(1) et CbL(
. La contrainte appliquée au graphe d'états
lie les valeurs des marquages associés à des états voisins (reliés
par une transition). Nous verrons qu'il existe une différence
entre les algorithmes Cb1(1) et CbL(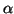 ), dans le cadre d'un
problème d'atteinte d'objectif. Néanmoins, cette différence
n'apparaît pas dans les propriétés essentielles de l'algorithme
CbL. Donc, nous ne considérerons dans un premier temps que
l'algorithme CbL(1). Les graphes d'états servant d'exemple
utiliseront l'équation 2.1 en prenant
), dans le cadre d'un
problème d'atteinte d'objectif. Néanmoins, cette différence
n'apparaît pas dans les propriétés essentielles de l'algorithme
CbL. Donc, nous ne considérerons dans un premier temps que
l'algorithme CbL(1). Les graphes d'états servant d'exemple
utiliseront l'équation 2.1 en prenant 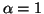 .
.




suivant: Algorithme d'apprentissage CbL
monter: Description de l'algorithme CbL
précédent: Marquage des états du
Table des matières
2002-03-01