La figure montre l'ensemble S(t) à l'instant t=3.5 s, qui est
composé de deux hypothèses, dont les focus sont représentés par
les deux parallélogrammes en trait épais, de génératrices 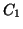 et
et 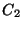 . Ces deux hypothèses ont été générées aux instant t=2 s
et t=2.7 s . . Ces deux hypothèses ont été générées aux instant t=2 s
et t=2.7 s . |
![\includegraphics[]{fig/recons.eps}](img257.png)
![\includegraphics[]{fig/recons.eps}](img257.png)