



suivant: Précisions concernant l'algorithme de
monter: Algorithme de sélection pour
précédent: Introduction
Table des matières
L'ensemble des hypothèses sera noté M =
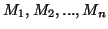
![[*]](file:/usr/lib/latex2html/icons/footnote.png) . Une hypothèse
. Une hypothèse 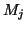 est associée à une fonction
génératrice
est associée à une fonction
génératrice 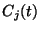 , ainsi qu'au triplet (
, ainsi qu'au triplet (
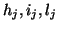 ). L'algorithme
de sélection peut être rapproché d'un problème d'exploration/exploitation
sur une période de temps finie. En effet, il possède deux fonctions
antagonistes qui s'exercent à chaque instant t: une génération d'hypothèses,
qui tend à augmenter le nombre d'hypothèses qui doivent être testées à chaque
instant, et une élimination d'hypothèses. Nous allons expliciter ces deux parties.
). L'algorithme
de sélection peut être rapproché d'un problème d'exploration/exploitation
sur une période de temps finie. En effet, il possède deux fonctions
antagonistes qui s'exercent à chaque instant t: une génération d'hypothèses,
qui tend à augmenter le nombre d'hypothèses qui doivent être testées à chaque
instant, et une élimination d'hypothèses. Nous allons expliciter ces deux parties.
La génération d'hypothèses est très simple. Elle a pour but d'explorer
l'ensemble des possibilités d'évolution du signal contenues dans la mémoire.
Pour cela, à chaque instant t, on génère l'ensemble total des hypothèses,
noté E(t): E(t) = M. On ajoute cet ensemble à l'ensemble, noté TE(t), des
ensembles E(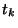 ), pour
), pour
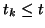 , coexistant à cet instant t. Par
conséquent, à chaque instant t, l'ensemble total des hypothèses considérées
est augmenté du cardinal de M, c'est-à-dire n.
, coexistant à cet instant t. Par
conséquent, à chaque instant t, l'ensemble total des hypothèses considérées
est augmenté du cardinal de M, c'est-à-dire n.
Voici comment fonctionne l'élimination d'hypothèses. À chaque instant t,
on récupère la valeur du signal X(t) et on regarde, pour chacune des hypothèses
de TE(t) ![[*]](file:/usr/lib/latex2html/icons/footnote.png) , si cette valeur appartient au focus associé à cette hypothèse. Si ce
n'est pas le cas, on incrémente un compteur d'erreur,
, si cette valeur appartient au focus associé à cette hypothèse. Si ce
n'est pas le cas, on incrémente un compteur d'erreur,
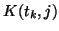 , qui est
propre à l'hypothèse
, qui est
propre à l'hypothèse 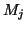 de l'ensemble E(
de l'ensemble E(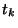 ). Ainsi, on va pouvoir
éliminer des éléments
). Ainsi, on va pouvoir
éliminer des éléments 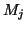 de E(t), pour deux raisons: soit
de E(t), pour deux raisons: soit 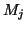 ne
respecte pas sa contrainte (
ne
respecte pas sa contrainte (
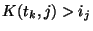 ), soit la durée de validation
), soit la durée de validation
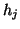 est atteinte (
est atteinte (
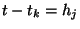 ) et l'hypothèse
) et l'hypothèse 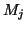 , formulée à un
instant
, formulée à un
instant 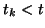 , est validée. Lorsqu'une hypothèse, formulée à un instant
, est validée. Lorsqu'une hypothèse, formulée à un instant
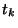 est soit validée, soit invalidée, on la retire de l'ensemble
est soit validée, soit invalidée, on la retire de l'ensemble 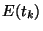 .
Si cet ensemble devient vide (on a retiré l'ensemble des hypothèses), on retire
l'ensemble
.
Si cet ensemble devient vide (on a retiré l'ensemble des hypothèses), on retire
l'ensemble 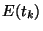 de l'ensemble TE(t). La procédure d'élimination permet de
conserver un ensemble réduits d'hypothèses qui traduisent l'évolution réelle
du signal. Ces hypothèses pourront être exploitées pour former une
information perceptive.
de l'ensemble TE(t). La procédure d'élimination permet de
conserver un ensemble réduits d'hypothèses qui traduisent l'évolution réelle
du signal. Ces hypothèses pourront être exploitées pour former une
information perceptive.
Lorsqu'une hypothèse est validée, on l'ajoute à l'ensemble S(t) qui contient
les hypothèses validées à l'instant t (et uniquement à l'instant t).
Les deux processus de génération et d'élimination d'hypothèses
forment l'algorithme de sélection 1.1.





suivant: Précisions concernant l'algorithme de
monter: Algorithme de sélection pour
précédent: Introduction
Table des matières
2002-03-01
