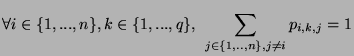suivant: Contexte idéal et quasi-idéal
monter: Outils d'étude de l'incertitude
précédent: Qu'entendons-nous par ``qualité'' du
Table des matières
On considère un ensemble de n états
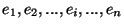 ,
ainsi qu'un ensemble de q actions
,
ainsi qu'un ensemble de q actions
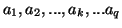 .
À chaque instant t, le système se trouve dans un état
.
À chaque instant t, le système se trouve dans un état  et choisit
d'exécuter une action
et choisit
d'exécuter une action 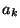 jusqu'à ce qu'il se trouve dans un état
jusqu'à ce qu'il se trouve dans un état
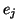 différent de
différent de  , à l'instant t+h. On considère également
l'état transitoire
, à l'instant t+h. On considère également
l'état transitoire  dans lequel le système se trouve entre
les instants t et t+h. Il faut donc distinguer l'état
dans lequel le système se trouve entre
les instants t et t+h. Il faut donc distinguer l'état  du système
alors qu'il n'a pas fait son choix sur l'action à exécuter, l'état
du système
alors qu'il n'a pas fait son choix sur l'action à exécuter, l'état
 pour lequel le système a fait son choix à partir de l'état
pour lequel le système a fait son choix à partir de l'état  et l'état
et l'état 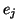 qui résulte de l'exécution de
qui résulte de l'exécution de 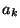 à partir de
à partir de  .
.
Les probabilités pour que le système se trouve respectivement dans
l'état  et
et  seront notées
seront notées 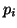 (resp.
(resp.
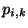 ). Pour un état
). Pour un état  et une action
et une action 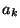 fixés, on
considère l'ensemble des probabilités
fixés, on
considère l'ensemble des probabilités 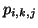 d'atteindre les
autres états du système, à l'exception de
d'atteindre les
autres états du système, à l'exception de  , grâce à
l'action
, grâce à
l'action 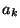 . Nous avons la relation:
. Nous avons la relation:




suivant: Contexte idéal et quasi-idéal
monter: Outils d'étude de l'incertitude
précédent: Qu'entendons-nous par ``qualité'' du
Table des matières
2002-03-01