



suivant: Exemples de contextes vérifiant
monter: Outils d'étude de l'incertitude
précédent: Notations
Table des matières
Contexte idéal et quasi-idéal - Propriété (
 )
)
Nous supposons que le contexte idéal
possède la propriété (P) suivante: Pour tout état
 du système et toute action
du système et toute action 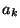 disponible lorsque le
système est dans l'état
disponible lorsque le
système est dans l'état  , toutes les probabilités
, toutes les probabilités
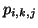 sont nulles à l'exception d'une seule qui vaut 1. De
même, pour tout état
sont nulles à l'exception d'une seule qui vaut 1. De
même, pour tout état  du système, si une action
du système, si une action 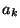 amène celui-ci dans l'état
amène celui-ci dans l'état 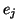 , alors aucune autre action ne
peut l'amener dans l'état
, alors aucune autre action ne
peut l'amener dans l'état 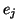 .
Cela signifie qu'à partir de l'état
.
Cela signifie qu'à partir de l'état  , il est possible de prédire
avec une parfaite exactitude le résultat de l'action
, il est possible de prédire
avec une parfaite exactitude le résultat de l'action 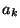 sur
l'évolution de l'état du système et que si on connaît deux états
consécutifs
sur
l'évolution de l'état du système et que si on connaît deux états
consécutifs  et
et 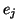 , alors on sait en déduire avec exactitude
l'action exécutée à partir de l'état
, alors on sait en déduire avec exactitude
l'action exécutée à partir de l'état 
En marge de ce contexte idéal, nous allons plus particulièrement
nous intéresser à un ensemble de contextes quasi-idéaux,
respectant la propriété (
 ) suivante:
On considère une valeur réelle
) suivante:
On considère une valeur réelle 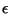 strictement positive et
très proche de 0. Pour tout état
strictement positive et
très proche de 0. Pour tout état  du système et toute
action
du système et toute
action 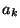 disponible lorsque le système est dans l'état
disponible lorsque le système est dans l'état
 , toutes les probabilités
, toutes les probabilités 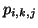 sont inférieures à
sont inférieures à
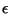 à l'exception d'une seule qui est supérieure à
à l'exception d'une seule qui est supérieure à
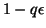 . De même, pour tout état
. De même, pour tout état  et tout état consécutif
et tout état consécutif
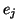 du système, les probabilités
du système, les probabilités 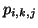 sont toutes
inférieures à
sont toutes
inférieures à 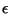 sauf une qui est supérieure à
sauf une qui est supérieure à
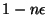 .
Si
.
Si 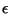 est suffisamment petit, le contexte quasi-idéal
se comporte en pratique (dans la durée de l'expérience) comme le
contexte idéal: la probabilité de découvrir deux transitions différentes
à partir d'un même état transitoire
est suffisamment petit, le contexte quasi-idéal
se comporte en pratique (dans la durée de l'expérience) comme le
contexte idéal: la probabilité de découvrir deux transitions différentes
à partir d'un même état transitoire  est si faible, que la
réalisation de cet événement n'arrive pas dans la durée de l'expérience.
De même, la probabilité pour que deux actions différentes exécutées à partir
d'un état
est si faible, que la
réalisation de cet événement n'arrive pas dans la durée de l'expérience.
De même, la probabilité pour que deux actions différentes exécutées à partir
d'un état  amènent au même état
amènent au même état 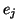 est si faible que cela
n'arrive pas en pratique.
est si faible que cela
n'arrive pas en pratique.
Dans la suite de notre discours, nous confondrons les propriétés
(P) et (
 ) en utilisant uniquement le terme
``(
) en utilisant uniquement le terme
``(
 )''.
)''.




suivant: Exemples de contextes vérifiant
monter: Outils d'étude de l'incertitude
précédent: Notations
Table des matières
2002-03-01