![\includegraphics[]{fig/res_H_entree.eps}](img107.png)
Légende:
``EVH'' Évolution de la Valeur de  et de et de 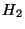 (abscisses:
amplitude du bruit de mesure, taux de valeurs aléatoires [0.1 = 10%];
ordonnées: valeur normalisée de (abscisses:
amplitude du bruit de mesure, taux de valeurs aléatoires [0.1 = 10%];
ordonnées: valeur normalisée de  et/ou de et/ou de 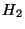 ). ).
``EHMR'' Évolution de la valeur de  en fonction du taux de
Mauvaise Reconnaissance de l'état courant du système. en fonction du taux de
Mauvaise Reconnaissance de l'état courant du système.
``DG'' Données issues de 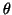 bruitées avec un bruit gaussien,
d'amplitude bruitées avec un bruit gaussien,
d'amplitude 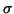 . .
``DVA'' Données issues de  possédant un taux de valeurs
aberrantes possédant un taux de valeurs
aberrantes 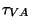 . .
``EA'' L'état du système peut être choisi aléatoirement, avec une
fréquence d'apparition 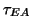 . .
Commentaires:
Les graphes (a),(b) et (c) montrent l'évolution des valeurs de
 et et 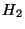 lorsque l'amplitude du bruit de mesure
augmente, suivant les trois types de bruits. Les graphes (d), (e)
et (f) sont construits respectivement à partir de (a), (b) et (c),
en considérant une échelle log/log. L'intérêt est de contater que
lorsque l'amplitude du bruit est faible, lorsque l'amplitude du bruit de mesure
augmente, suivant les trois types de bruits. Les graphes (d), (e)
et (f) sont construits respectivement à partir de (a), (b) et (c),
en considérant une échelle log/log. L'intérêt est de contater que
lorsque l'amplitude du bruit est faible,  peut se mettre
sous la forme peut se mettre
sous la forme
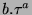 , avec , avec 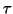 l'amplitude du bruit de
mesure, et a et b les paramètres des droites constatées dans les
graphes (d),(e) et (f) lorsque l'amplitude du bruit de
mesure, et a et b les paramètres des droites constatées dans les
graphes (d),(e) et (f) lorsque 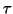 est suffisamment faible.
Enfin, les graphes (g), (h) et (i) montrent qu'il existe une
relation fonctionnelle entre le taux de mauvaise reconnaissance de
l'état courant du système et la valeur de est suffisamment faible.
Enfin, les graphes (g), (h) et (i) montrent qu'il existe une
relation fonctionnelle entre le taux de mauvaise reconnaissance de
l'état courant du système et la valeur de  . On s'aperçoit
que s'il existe une corrélation quasi-linéaire pour un bruit
``DG'', pour les deux autres bruits, . On s'aperçoit
que s'il existe une corrélation quasi-linéaire pour un bruit
``DG'', pour les deux autres bruits,  augmente beaucoup
plus vite que le taux de mauvaise reconnaissance. augmente beaucoup
plus vite que le taux de mauvaise reconnaissance.
|
![\includegraphics[]{fig/res_H_entree.eps}](img107.png)