Signification de la valeur des marquages

Une particularité de l'algorithme CbL est que la valeur du marquage d'un état $e_{i}$ est directement liée à la fiabilité de la politique de commande empruntant $e_{i}$. À ce sujet, voici trois propositions intéressantes:

Proposition _s   lorsque le système respecte ( $P_{\epsilon }$), le marquage $M_{i}$ d'un état $e_{i}$ vaut 1 dans l'unique cas où il existe au moins une politique de commande empruntant $e_{i}$ parvenant à coup sûr à l'objectif $E_{S}$.

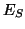
Proposition _s   lorsque le problème de choix de commande est markovien, le marquage $M_{i}$ d'un état $e_{i}$ vaut -1 dans le cas où aucune politique de commande empruntant $e_{i}$ ne peut éviter $E_{E}$.

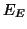
Proposition _s   Pour un problème de viabilité, si on constate à un moment de l'apprentissage qu'il existe des états formant un cycle ou plusieurs cycles, dont les marquages possèdent une qualité 0, cela signifie que la politique de commande associée au parcours de ce ou ces cycles n'a jamais échoué jusqu'à ce moment précis.

Pour prouver la proposition 2, il suffit de montrer qu'il existe un chemin de l'état $e_{i}$ vers l'état $E_{S}$, déterminé uniquement par la séquence des états transitoires choisis (c'est-à-dire des actions sélectionnées). Dans le cas où le système respecte ( $P_{\epsilon }$), nous avons montré que la résolution de proche en proche du système d'équations à partir des états liés à $E_{S}$ détermine l'intégralité des marquages à 1. Or, la résolution de proche en proche emprunte les transitions existant dans le graphe entre les états $e_{i,k}$ et les états $e_{j}$. Donc, pour chaque état possédant un marquage 1, il existe un chemin vers l'état $E_{S}$. Ce chemin est déterminé par la connaissance des commandes appliquées car l'hypothèse ( $P_{\epsilon }$) indique qu'un état $e_{i}$ et une action $a_{k}$ conditionnent l'état résultant $e_{j}$. Par conséquent, si on connaît l'état $e_{i}$, une séquence de commandes détermine précisément le parcours dans le graphe d'états. Ce qui montre la proposition 2.
Pour montrer la proposition 3, nous allons d'abord constater que, s'il existe au moins un état $e_{i}$ de qualité -1, alors il existe un $e_{j}$ pour lequel il existe une probabilité non nulle que l'état suivant soit $E_{E}$. En effet, la qualité -1 est obtenue forcément par la résolution de proche en proche du système d'équations (d'après la proposition 1); elle ne peut s'amorcer à partir de l'état $E_{E}$ que s'il existe un marquage $M_{j}$ tel que l'ensemble des $M_{j,k}$ soient égaux à -1. Et cela n'est possible que si, quelle que soit la commande choisie, il existe une transition vers $E_{E}$. Par conséquent, lorsque le système se situe dans l'état $e_{j}$, la probabilité $p_{j}$ pour qu'il arrive en $E_{E}$ est non nulle. Et, grâce à l'hypothèse markovienne, $p_{j}$ ne dépend que de la présence du système dans l'état $e_{j}$. Ce dernier joue alors le même rôle que l'état $E_{E}$. Si $e_{i}$ est différent de $e_{j}$, on montre de même qu'il existe un état $e_{l}$ dont la probabilité de transition $p_{l}$ vers $E_{j} \bigcup E_{E}$ est non nulle, quelle que soit la commande choisie en $e_{l}$. Or, l'aboutissement à $e_{j}$ conduit avec une probabilité $p_{j}$ vers $E_{E}$. Cela implique qu'il existe une probabilité non nulle $p_{l}.p_{j}$ d'atteindre $E_{E}$ à partir de $e_{l}$. Le même raisonnement est appliqué jusqu'à ce que $e_{i}$ fasse partie de l'ensemble des états pour lesquels la probabilité d'atteindre $E_{S}$ est non nulle. Cela se termine forcément puisque le nombre d'états du système est fini.
La proposition 4 se montre utilisant le fait qu'à partir d'un état $e_{i}$ de qualité 0 faisant partie d'un cycle, il existe une commande pour laquelle les transitions associées aboutissent toutes à des états de qualité 0 (dans le cas contraire, la qualité de $e_{i}$ serait à -1).