



suivant: Signification de la valeur
monter: Résultats théoriques concernant l'algorithme
précédent: Convergence de la phase
Table des matières
Nous allons montrer les points suivants, regroupés sous la forme d'une proposition
Proposition _s
- dans le cas général, l'historique de l'ajout des transitions
influe sur la valeur des marquages obtenus au cours de l'apprentissage
- dans le cas particulier où le système respecte la propriété
(
 ), il existe un lien fonctionnel entre le graphe
d'états (états et transitions) et la valeur des marquages
associés: cela montre l'unicité de l'ensemble des valeurs de
marquage obtenues grâce à l'algorithme d'apprentissage
), il existe un lien fonctionnel entre le graphe
d'états (états et transitions) et la valeur des marquages
associés: cela montre l'unicité de l'ensemble des valeurs de
marquage obtenues grâce à l'algorithme d'apprentissage
- dans le cas particulier où il n'existe aucune transition vers
l'état
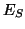 (problème de viabilité), il n'est pas nécessaire
que la propriété (
(problème de viabilité), il n'est pas nécessaire
que la propriété (
 ) soit respectée pour obtenir ce
lien fonctionnel
) soit respectée pour obtenir ce
lien fonctionnel
Nous allons débuter cette sous-section en montrant les limites du
contexte pour lequel il existe une unicité de l'ensemble des
valeurs de marquage lorsque le graphe d'états est fixé (états et
transitions). La résolution du système d'équations
2.1, pour des valeurs de  et
et  dans
0,1,-1, et un ensemble de transitions fixé, aboutit dans le cas
général à plusieurs solutions. La figure 2.3
illustre ce fait, en présentant deux graphes d'états cohérents,
possédant les mêmes transitions mais pas les mêmes marquages
(graphes (a) et (b)). Pourtant, on sent intuitivement que le
graphe (b) ne peut pas être obtenu en utilisant l'algorithme
d'apprentissage CbL. En effet, la valeur d'initialisation des
marquages étant nulle, on ne voit pas comment il pourrait exister
un passage à la valeur 1 sans qu'il existe une transition vers
l'état
dans
0,1,-1, et un ensemble de transitions fixé, aboutit dans le cas
général à plusieurs solutions. La figure 2.3
illustre ce fait, en présentant deux graphes d'états cohérents,
possédant les mêmes transitions mais pas les mêmes marquages
(graphes (a) et (b)). Pourtant, on sent intuitivement que le
graphe (b) ne peut pas être obtenu en utilisant l'algorithme
d'apprentissage CbL. En effet, la valeur d'initialisation des
marquages étant nulle, on ne voit pas comment il pourrait exister
un passage à la valeur 1 sans qu'il existe une transition vers
l'état 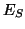 . Cependant, on ne peut pas déduire cela du système
d'équations. En effet, le voici:
. Cependant, on ne peut pas déduire cela du système
d'équations. En effet, le voici:
La résolution de ce système s'effectue de proche en proche. Il vient:
On en déduit qu'il existe deux ensembles de solutions, représentés
par le graphe (a) (solutions engendrées en fixant 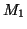 à 0) et
le graphe (b) (
à 0) et
le graphe (b) (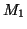 = 1).
= 1).
Le graphe (c) montre par quelle manière on peut passer du schéma (a)
au schéma (b): ajouter une transition vers l'état 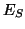 (en pointillé
sur la partie gauche du graphe (c)), donne le schéma de droite du graphe
(c) en utilisant l'algorithme de propagation, puis la supprimer redonne
le graphe (b), toujours en utilisant l'algorithme de propagation. Or,
l'algorithme d'apprentissage ne fonctionne que par ajout de transition.
Cet exemple montre que, dans le cas général où on autorise également des
suppressions de transitions, la valeur des marquages dépend de l'historique
des opérations d'ajout et de suppression.
(en pointillé
sur la partie gauche du graphe (c)), donne le schéma de droite du graphe
(c) en utilisant l'algorithme de propagation, puis la supprimer redonne
le graphe (b), toujours en utilisant l'algorithme de propagation. Or,
l'algorithme d'apprentissage ne fonctionne que par ajout de transition.
Cet exemple montre que, dans le cas général où on autorise également des
suppressions de transitions, la valeur des marquages dépend de l'historique
des opérations d'ajout et de suppression.
Les graphes (d) et (e) montrent que, dans le cas général de
construction du graphe d'état par apprentissage, la valeur des
marquages dépend de l'historique des opérations d'ajout de
transitions. Le graphe (d) montre qu'à partir d'un graphe cohérent
(partie gauche) dans lequel le marquage des deux états est à 1,
l'ajout de la transition de 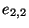 vers
vers 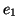 (en pointillés)
ne change pas la cohérence du graphe. D'autre part, le graphe (e)
est cohérent, avec le marquage des états valant 0 (figure de
gauche); l'ajout de la transition de
(en pointillés)
ne change pas la cohérence du graphe. D'autre part, le graphe (e)
est cohérent, avec le marquage des états valant 0 (figure de
gauche); l'ajout de la transition de 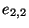 vers
vers 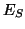 ne
change pas la cohérence du graphe. Or, les graphes d'état des deux
figures de droite sont identiques, alors que leurs marquages sont
différents.
ne
change pas la cohérence du graphe. Or, les graphes d'état des deux
figures de droite sont identiques, alors que leurs marquages sont
différents.
Figure:
Exemples de cas de multiplicité des solutions au problème de marquage
|
|
Après avoir fourni ces contre-exemples utiles à une première
compréhension des mécanismes de propagation, nous souhaitons montrer
que, dans le cadre de l'application de l'algorithme d'apprentissage pour
un système vérifiant la propriété (
 ), la valeur des
marquages ne dépend pas de l'historique des opérations d'ajout de
transitions, conditionné par la stratégie d'exploration des états. Ce
résultat est important, car il permet de voir la valeur des marquages
obtenue après apprentissage comme une fonction de l'ensemble des transitions
découvertes. Par conséquent, la connaissance de ces transitions suffit pour
déterminer la valeur des marquages.
), la valeur des
marquages ne dépend pas de l'historique des opérations d'ajout de
transitions, conditionné par la stratégie d'exploration des états. Ce
résultat est important, car il permet de voir la valeur des marquages
obtenue après apprentissage comme une fonction de l'ensemble des transitions
découvertes. Par conséquent, la connaissance de ces transitions suffit pour
déterminer la valeur des marquages.
Prouvons la validité du deuxième point de la proposition 1,
en utilisant les équations de la relation 2.1 liant le marquage
des états  à celui des états
à celui des états  . Pour cela, nous allons établir
une formulation modifiée de ce système d'équations.
. Pour cela, nous allons établir
une formulation modifiée de ce système d'équations.
Commençons par les équations liées aux états transitoires
 . Celles-ci sont très simplifiées puisque l'hypothèse
(
. Celles-ci sont très simplifiées puisque l'hypothèse
(
 ) stipule qu'une transition d'un état
) stipule qu'une transition d'un état  ne
peut aboutir qu'à un unique état
ne
peut aboutir qu'à un unique état 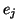 ou à un état terminal.
L'expression du marquage
ou à un état terminal.
L'expression du marquage  prend quatre formes
différentes:
prend quatre formes
différentes:
 n'est relié à aucun état
n'est relié à aucun état 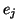 . Dans ce cas, l'équation
associée à
. Dans ce cas, l'équation
associée à  se résume, par hypothèse, à:
se résume, par hypothèse, à:  = 0
= 0
 est relié à
est relié à 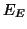 . Dans ce cas, l'équation se résume à:
. Dans ce cas, l'équation se résume à:  = -1
= -1
 est relié à
est relié à 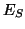 . Dans ce cas, il vient:
. Dans ce cas, il vient:  = 1
= 1
 ne répond à aucun des trois cas précédents.
ne répond à aucun des trois cas précédents.  =
= 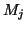
Occupons-nous à présent des équations associées aux états  .
En injectant l'expression des
.
En injectant l'expression des  dans celle de
dans celle de  , on
trouve quatre cas distincts:
, on
trouve quatre cas distincts:
- un
 vaut 1, ce qui entraîne que, quel que soit l'expression des
marquages associés aux autres états
vaut 1, ce qui entraîne que, quel que soit l'expression des
marquages associés aux autres états  , on a l'équation:
, on a l'équation:  = 1
= 1
- l'ensemble des marquages associés aux états transitoires sont fixés à 0
ou -1. Dans ce cas,
 = c, avec c valant 0 ou -1.
= c, avec c valant 0 ou -1.
- l'ensemble des marquages associés aux états transitoires ne comporte que
des marquages étant réductibles à un
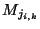 avec
éventuellement des marquages valant -1. Dans ce cas, il vient:
avec
éventuellement des marquages valant -1. Dans ce cas, il vient:
 =
= 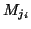 , avec
, avec 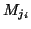 = max
= max
- dans les autres cas de figure, il existe des marquages valant 0, ce
qui modifie l'expression précédente:
 = max{0,
= max{0, 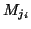 }
}
La valeur d'un  peut donc être directement connue (cas 1 et
2) ou être en relation avec celle d'un autre marquage (cas 3 et
4). La résolution du système s'effectue soit directement, pour des
états qui ne sont pas connectés à d'autres états (cas 1), soit de
proche en proche à partir des états connectés aux états terminaux
peut donc être directement connue (cas 1 et
2) ou être en relation avec celle d'un autre marquage (cas 3 et
4). La résolution du système s'effectue soit directement, pour des
états qui ne sont pas connectés à d'autres états (cas 1), soit de
proche en proche à partir des états connectés aux états terminaux
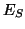 ou
ou 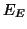 . Le problème de l'unicité des valeurs des
marquages
. Le problème de l'unicité des valeurs des
marquages  revient à savoir s'il peut rester des valeurs
indéterminées de
revient à savoir s'il peut rester des valeurs
indéterminées de  , répondant aux cas 3 ou 4, à la fin de la
résolution de proche en proche. L'exemple que nous avons présenté
en début de sous-section indique que cela peut arriver. Dans ce
cas, considérons l'ensemble M des marquages ne pouvant être
résolus: M = {
, répondant aux cas 3 ou 4, à la fin de la
résolution de proche en proche. L'exemple que nous avons présenté
en début de sous-section indique que cela peut arriver. Dans ce
cas, considérons l'ensemble M des marquages ne pouvant être
résolus: M = {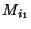 ,
, 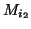 , ...,
, ..., 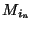 }. Pour
chaque
}. Pour
chaque
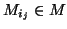 , les cas 3 et 4 imposent que:
, les cas 3 et 4 imposent que:
- soit il existe un
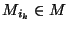 tel que
tel que
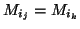 (cas 3)
(cas 3)
- soit il existe un
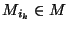 tel que
tel que
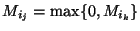 (cas 4)
(cas 4)
Le deuxième point correspond au cas évoqué par les graphes (a) et (b).
Il offre a priori deux solutions pour 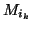 : 0 ou 1. Pour le
premier point,
: 0 ou 1. Pour le
premier point, 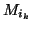 peut valoir a priori 0, 1 ou -1. Mais, tous
ces cas sont-ils possibles ?
peut valoir a priori 0, 1 ou -1. Mais, tous
ces cas sont-ils possibles ?
En premier lieu, il faut remarquer que l'utilisation des équations ne permet
de déduire qu'un marquage vaut 0 uniquement lorsque l'état associé ne possède
pas de transition vers un autre état. En effet, la résolution de proche en proche
s'effectue à partir des états terminaux 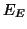 et
et 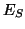 , ce qui permet de fixer
les valeurs des marquages à 1 ou -1. On en déduit que s'il existe des marquages
valant 0 dont l'état
, ce qui permet de fixer
les valeurs des marquages à 1 ou -1. On en déduit que s'il existe des marquages
valant 0 dont l'état  associé possède au moins une transition vers un
autre état
associé possède au moins une transition vers un
autre état 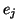 , alors ces marquages sont dans M. Mais, cela signifie-t-il
que tous les marquages de M sont nuls ?
, alors ces marquages sont dans M. Mais, cela signifie-t-il
que tous les marquages de M sont nuls ?
Prenons un état  dont le marquage est dans M.
dont le marquage est dans M.  ne peut pas avoir
de transitions vers un
ne peut pas avoir
de transitions vers un 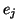 extérieur à M, de marquage connu
extérieur à M, de marquage connu 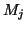 = 1. En
effet, dans ce cas, la valeur de
= 1. En
effet, dans ce cas, la valeur de  serait alors connue et fixée à 1 (cas 1).
Or, si un marquage
serait alors connue et fixée à 1 (cas 1).
Or, si un marquage  de M vaut 1, cela signifie que cette valeur a été
propagée par une transition aboutissant à l'état associé
de M vaut 1, cela signifie que cette valeur a été
propagée par une transition aboutissant à l'état associé  (puisque la
valeur initiale de
(puisque la
valeur initiale de  est 0). D'après la remarque précédente, cette
transition ne peut provenir que d'un élément de M. Ce qui reporte le problème
à un autre
est 0). D'après la remarque précédente, cette
transition ne peut provenir que d'un élément de M. Ce qui reporte le problème
à un autre  de M, d'où une non-résolution du problème dans l'hypothèse
d'un marquage de M valant 1. Cela montre l'impossibilité que les marquages de M
puissent être égaux à 1. Émettons l'hypothèse qu'un marquage
de M, d'où une non-résolution du problème dans l'hypothèse
d'un marquage de M valant 1. Cela montre l'impossibilité que les marquages de M
puissent être égaux à 1. Émettons l'hypothèse qu'un marquage  de M soit
égal à -1. Dans ce cas, il est régi par le cas 3 (le cas 4 est impossible). Le
passage du marquage de 0 à -1 n'est possible que si toutes les transitions issues
de
de M soit
égal à -1. Dans ce cas, il est régi par le cas 3 (le cas 4 est impossible). Le
passage du marquage de 0 à -1 n'est possible que si toutes les transitions issues
de 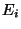 possèdent un marquage -1. Comme
possèdent un marquage -1. Comme  est dans M, il existe forcément
une transition menant à un marquage de M. Ce marquage doit donc avoir été mis à -1
précédemment. Comme dans le cas précédent, le problème du passage de la valeur de
est dans M, il existe forcément
une transition menant à un marquage de M. Ce marquage doit donc avoir été mis à -1
précédemment. Comme dans le cas précédent, le problème du passage de la valeur de
 de 0 à -1 est reporté sur un autre élément de M. Cela montre également
l'impossibilité de notre hypothèse
de 0 à -1 est reporté sur un autre élément de M. Cela montre également
l'impossibilité de notre hypothèse  = -1. Par conséquent, l'intégralité
des marquages de M ont une valeur 0.
= -1. Par conséquent, l'intégralité
des marquages de M ont une valeur 0.
Donc, nous venons de montrer l'unicité de la valeur des marquages obtenus par
l'algorithme de propagation, dans le cas où le système vérifie la propriété
(
 ).
).
Considérons à présent le cas particulier où il n'existe pas de transition
vers l'état 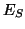 : il correspond à un problème de viabilité. Nous allons
montrer le même résultat que précédemment, mais sans utiliser la propriété
(
: il correspond à un problème de viabilité. Nous allons
montrer le même résultat que précédemment, mais sans utiliser la propriété
(
 ). Les modifications au niveau des équations sont peu
nombreuses: le cas 4 n'existe plus, puisque le fait qu'il n'existe pas
de transition à partir d'un
). Les modifications au niveau des équations sont peu
nombreuses: le cas 4 n'existe plus, puisque le fait qu'il n'existe pas
de transition à partir d'un  suffit pour montrer que le marquage
de
suffit pour montrer que le marquage
de  vaut 0. Le cas d'indétermination est donc uniquement le cas 3.
D'autre part, la propriété (
vaut 0. Le cas d'indétermination est donc uniquement le cas 3.
D'autre part, la propriété (
 ) n'est utilisée précédemment que
pour éliminer la possibilité d'une transition à partir d'un état associé à M
jusque vers un état de marquage 1 n'appartenant pas à M (c'est précisément le
cas montré par les graphes (d) et (e), pour lequel l'ordre d'apparition des
transitions change le marquage final). Dans notre cas, ce problème n'existe
plus. En effet, l'indétermination sur
) n'est utilisée précédemment que
pour éliminer la possibilité d'une transition à partir d'un état associé à M
jusque vers un état de marquage 1 n'appartenant pas à M (c'est précisément le
cas montré par les graphes (d) et (e), pour lequel l'ordre d'apparition des
transitions change le marquage final). Dans notre cas, ce problème n'existe
plus. En effet, l'indétermination sur  existe s'il existe au moins
une transition partant
existe s'il existe au moins
une transition partant  vers un état
vers un état 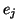 associé à M, sans
qu'il existe une transition de
associé à M, sans
qu'il existe une transition de  vers un état non associé à M
(dans le cas contraire, le minimum des deux marquages serait égal à -1,
quel que soit
vers un état non associé à M
(dans le cas contraire, le minimum des deux marquages serait égal à -1,
quel que soit 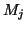 ). L'hypothèse
). L'hypothèse
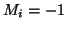 implique donc que
l'état
implique donc que
l'état  soit passé d'un marquage 0 à un marquage -1. Pour cela,
l'unique possibilité est que l'ensemble des transitions partant de
soit passé d'un marquage 0 à un marquage -1. Pour cela,
l'unique possibilité est que l'ensemble des transitions partant de
 aboutissent à des états marqués à -1. Or, nous venons de montrer
qu'il existe au moins une transition allant de
aboutissent à des états marqués à -1. Or, nous venons de montrer
qu'il existe au moins une transition allant de  vers un état
associé à M. Il faudrait donc que le marquage de celui-ci soit passé
préalablement d'un marquage 0 à un marquage -1. Ce qui reporte le problème
à un autre état associé à M. D'où la conclusion que les marquages indéterminés
par résolution de proche en proche sont égaux à 0. Ce qui termine la démonstration
du troisième point de la proposition 1.
vers un état
associé à M. Il faudrait donc que le marquage de celui-ci soit passé
préalablement d'un marquage 0 à un marquage -1. Ce qui reporte le problème
à un autre état associé à M. D'où la conclusion que les marquages indéterminés
par résolution de proche en proche sont égaux à 0. Ce qui termine la démonstration
du troisième point de la proposition 1.




suivant: Signification de la valeur
monter: Résultats théoriques concernant l'algorithme
précédent: Convergence de la phase
Table des matières
2002-03-01
 ), il existe un lien fonctionnel entre le graphe
d'états (états et transitions) et la valeur des marquages
associés: cela montre l'unicité de l'ensemble des valeurs de
marquage obtenues grâce à l'algorithme d'apprentissage
), il existe un lien fonctionnel entre le graphe
d'états (états et transitions) et la valeur des marquages
associés: cela montre l'unicité de l'ensemble des valeurs de
marquage obtenues grâce à l'algorithme d'apprentissage
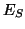 (problème de viabilité), il n'est pas nécessaire
que la propriété (
(problème de viabilité), il n'est pas nécessaire
que la propriété (
 ) soit respectée pour obtenir ce
lien fonctionnel
) soit respectée pour obtenir ce
lien fonctionnel
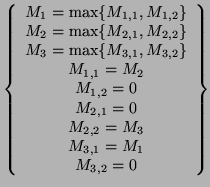
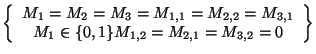
![\includegraphics[]{fig/multi_sol.eps}](img158.png)