



suivant: Cas d'unicité de l'ensemble
monter: Résultats théoriques concernant l'algorithme
précédent: Problèmes théoriques
Table des matières
Nous allons montrer que la phase de propagation se termine
toujours: il n'y a pas de bouclage au cours de la modification des
marquages  et
et  . Pour cela, il faut noter que nous n'avons
pas besoin de l'existence de la propriété (
. Pour cela, il faut noter que nous n'avons
pas besoin de l'existence de la propriété (
 ).
).
Soit S, la somme des marquages de l'ensemble des états perceptifs  et des états transitoires
et des états transitoires  . Considérons à présent la valeur de S
à l'instant t, notée S(t), et supposons qu'une nouvelle transition est
découverte à cet instant. Admettons que cette transition relie l'état
transitoire
. Considérons à présent la valeur de S
à l'instant t, notée S(t), et supposons qu'une nouvelle transition est
découverte à cet instant. Admettons que cette transition relie l'état
transitoire  à l'état perceptif
à l'état perceptif 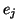 . La valeur de
. La valeur de  dépend donc d'un nouveau marquage
dépend donc d'un nouveau marquage 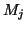 .
.
Deux cas se présentent:
- l'ajout de
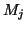 ne modifie pas le minimum des marquages des
états connectés à
ne modifie pas le minimum des marquages des
états connectés à 
- la valeur de
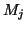 change le minimum des marquages des états connectés à
change le minimum des marquages des états connectés à 
Dans le premier cas, l'ajout de cette transition ne modifie pas la
cohérence au niveau de  et la phase de propagation n'est pas enclenchée.
et la phase de propagation n'est pas enclenchée.
Le second cas comporte deux sous-cas: soit la valeur minimum est
augmentée par l'ajout du marquage 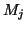 , soit elle est diminuée.
Nous allons montrer que, dans les deux cas, la suite des modifications
apportées aux marquages par la phase de propagation s'exprime par une
évolution monotone de S.
, soit elle est diminuée.
Nous allons montrer que, dans les deux cas, la suite des modifications
apportées aux marquages par la phase de propagation s'exprime par une
évolution monotone de S.
Dans chacun des deux cas,  doit être modifiée pour
respecter la cohérence au niveau de l'état
doit être modifiée pour
respecter la cohérence au niveau de l'état  . La valeur de
. La valeur de
 est mise à
est mise à 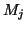 . Supposons que cette modification
rende la nouvelle valeur de
. Supposons que cette modification
rende la nouvelle valeur de  inférieure à la précédente:
la nouvelle valeur S(t+1) est alors également inférieure à S(t)
après cette modification. Examinons à présent la cohérence au
niveau de l'état
inférieure à la précédente:
la nouvelle valeur S(t+1) est alors également inférieure à S(t)
après cette modification. Examinons à présent la cohérence au
niveau de l'état  . Deux cas de figure existent:
. Deux cas de figure existent:
- la modification de
 n'affecte pas le maximum des marquages
des états
n'affecte pas le maximum des marquages
des états  connectés à l'état
connectés à l'état 
- la valeur de
 change ce maximum
change ce maximum
Dans le premier cas, la phase de propagation se termine, avec
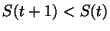 .
.
Dans le second cas, la valeur de  est incohérente. Or, le
rétablissement de la cohérence, sachant que la nouvelle valeur de
est incohérente. Or, le
rétablissement de la cohérence, sachant que la nouvelle valeur de  est inférieure à la précédente, se traduit par une diminution de la valeur de
est inférieure à la précédente, se traduit par une diminution de la valeur de
 , donc par une diminution de S: S(t+2) < S(t+1). Nous reprenons alors
l'étape de modification au niveau de chaque état transitoire connecté à
, donc par une diminution de S: S(t+2) < S(t+1). Nous reprenons alors
l'étape de modification au niveau de chaque état transitoire connecté à  .
Et chacune de ces étapes conduit soit à une diminution de S, soit à un S inchangé
(cas d'arrêt d'une branche de la phase de propagation). Par conséquent, la suite
(S(t)) est décroissante. Comme la valeur de S est minorée par -n.(q+1)
.
Et chacune de ces étapes conduit soit à une diminution de S, soit à un S inchangé
(cas d'arrêt d'une branche de la phase de propagation). Par conséquent, la suite
(S(t)) est décroissante. Comme la valeur de S est minorée par -n.(q+1)
![[*]](file:/usr/lib/latex2html/icons/footnote.png) , on en déduit que la suite (S(t)) converge, ce qui signifie
que la phase de propagation s'arrête.
, on en déduit que la suite (S(t)) converge, ce qui signifie
que la phase de propagation s'arrête.
Le même raisonnement peut être tenu lorsque la nouvelle valeur de  est supérieure à la précédente. Dans ce cas, la suite (S(t)) est croissante.
Or, elle est majorée par n.(q+1), donc elle converge.
est supérieure à la précédente. Dans ce cas, la suite (S(t)) est croissante.
Or, elle est majorée par n.(q+1), donc elle converge.
Nous venons de montrer que la phase de propagation se termine
toujours. Chaque état pour lequel la phase de propagation
s'arrête est cohérent, par construction. Par conséquent, le fait
de montrer que la propagation se termine est équivalent à dire que
le graphe est cohérent après la phase de propagation.




suivant: Cas d'unicité de l'ensemble
monter: Résultats théoriques concernant l'algorithme
précédent: Problèmes théoriques
Table des matières
2002-03-01