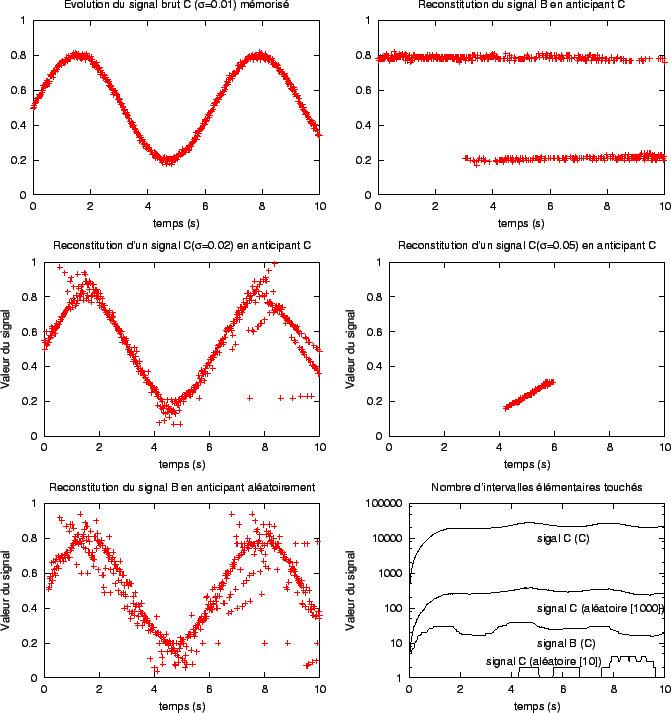
Pour les expériences résumées par l'ensemble des figures ci-dessus, nous avons limité l'ensemble des triplets possibles (h,i,l) à 8 possibilités: (71,56,0.01), (181,160,0.01), (32,18,0.02), (82,62,0.02), (215,186,0.02), (393,354,0.02), (22,8,0.03), (51,32,0.03). Ces triplets ont été choisis sur une valeur de l croissante (tous les triplets associés à l=0.01, puis ceux associés à l=0.02 et les deux premiers associés à l=0.03). Ils permettent théoriquement de supporter des signaux possédant un bruit gaussien de 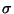 inférieur ou égal à 0.02 . inférieur ou égal à 0.02 .
Pour les différentes courbes, on indique le signal reçu par le système puis, entre parenthèses, le signal anticipé. La mention ``aléatoire'' signifie qu'on anticipe au hasard; le nombre entre crochets indique le nombre de zones sélectionnées à chaque pas de temps. |