6 Premiers résultats expérimentaux - nouvelle proposition

Dans ces premières expériences, nous allons considérer que le processus d'anticipation n'influence pas le processus d'élagage: cela signifie que UP_init est égal à l'espace des variables internes en entier: les limites de cet espace sont données par les contraintes C_{b, 0} et C_{a, 0} de l'équation 3.2). Donc, la surface S_init(t) est égale à 1 à chaque instant t. D'autre part, le paramètre $\epsilon$ est fixé à 10^-15.
Voici la liste des expérimentations préliminaires que nous avons effectuées:

1. Application d'un signal aléatoire U[0,1]
2. Étude à partir d'un signal sinusoïdal
   • un premier exemple de l'évolution de UP_fin(t) suivant le temps.
   • influence du bruit de mesure sur l'aire totale balayée ( réunion des S_fin(t) pour chaque instant t).
3. Étude à partir d'un signal issu d'une fonction discontinue
   • mise en évidence du fonctionnement du processus d'élagage à partir d'une fonction continue par morceaux
   • mise en défaut de l'algorithme fixant le choix de h à partir d'une fonction non continue par morceaux
4. Importance du choix de h pour discriminer deux signaux

Pour la première expérimentation, nous avons soumis le processus d'élagage à un signal de densité U[0,1] pendant 10 millions d'itérations. Nous avons constaté que, pendant ce temps, la valeur du signal de certitude reste constamment à 0, ce qui est cohérent avec la théorie. Cela tend à confirmer que le dimensionnement des focus est correct.
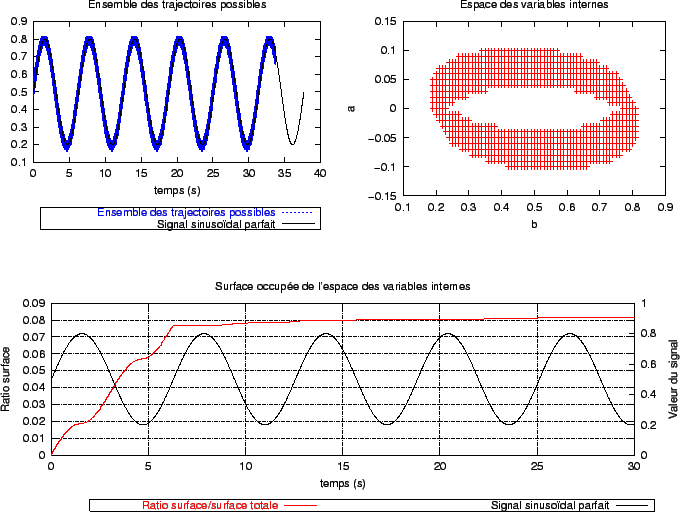
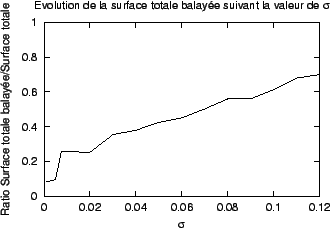
La figure 3.5 montre les résultats de la deuxième expérimentation en utilisant un signal sinusoïdal parfait (non bruité), alors que la figure 3.6 relate la même expérience pour un signal sinusoïdal bruité artificiellement. L'aire de la surface totale balayée au cours du temps est notablement plus importante dans le cas où le signal est bruité: cette augmentation s'explique par un accroissement du nombre des scenarii possibles pour une valeur de h donnée, mais aussi par une augmentation des valeurs de h utilisées. D'autre part, l'évolution de la surface totale balayée n'est pas stoppée après la première période du signal: il faut plus de temps pour voir apparaître l'ensemble des scenarii possibles. Cela signifie en particulier que, pour une même configuration du signal, certains scenarii possèdent une probabilité d'être validés qui n'est pas très proche de 0 ou très proche de 1. Or, comme nous l'avons déjà remarqué au cours du chapitre 2, il existe une certaine ``liberté'' des trajectoires des focus autour de la trajectoire suivie par le maximum de la densité de probabilité du signal: celle-ci se traduit par l'existence de scenarii ``limites''. Ceux-ci sont en partie à l'origine de l'importance de la surface de l'espace des variables internes balayée au cours du temps ( figure 3.7). Cette surface devient rapidement très importante et la restitution du signal à partir de l'ensemble des scenarii validés au cours du temps devient grossière.

Figure: Mise en oeuvre de l'algorithme d'élagage sur un signal sinusoïdal parfait.

La figure du bas montre que la surface balayée dans l'espace des variables internes vraie très peu à partir de la fin de la première période de la sinusoïde.

Figure: Mise en oeuvre de l'algorithme d'élagage sur un signal sinusoïdal bruité artificiellement.

Figure: Evolution de la surface totale balayée au cours du temps en fonction du paramètre sigma.

Les signaux étudiés ont une densité de probabilité gaussienne, de paramètre $\sigma$.

Ces premières expériences amènent deux questions:

1. La reconstitution d'un signal à partir d'un ensemble de scenarii validés au cours du temps semble décevante, car grossière. Peut-on distinguer, au sein de cet ensemble, des scenarii plus valides que d'autres (éliminer les cas ``limites''), de manière à reconstituer le signal plus fidèlement ?
2. L'algorithme d'élagage permet de passer de l'espace de perception à l'espace des variables internes. Nous avons vu qu'à partir d'un ensemble de scenarii, on peut reconstituer un signal, en passant de l'espace des variables internes à un espace identique à celui de l'espace de perception. Que se passerait-il si on poursuivait ce bouclage (espace de perception/espace des variables internes) en réinjectant le signal reconstitué dans le processus d'élagage (voir la figure 3.8) ? Quelle signification cela aurait-il ?

Figure 3.8: Bouclage espace perceptif/espace des variables internes.

La réponse à ces deux questions est délicate, en fait. En effet, notre attention se porte vers la ``qualité'' de la reconstitution du signal et, pour parvenir à une meilleure qualité, nous sommes tentés d'échafauder des critères de sélection non justifiés par nos hypothèses fondatrices et, en particulier, par l'exigence d'une quasi-certitude (première question). D'autre part, nous voyons le mécanisme de bouclage interne comme une possibilité d'améliorer également le ``rendu'' de la reconstitution du signal (deuxième question).
Avant de donner un exemple de réponse concrète à ces deux questions, nous remarquons que cette volonté d'obtenir une reconstitution de bonne qualité signifie que nous souhaitons que les données perçues soient filtrées de manière à obtenir, au bout du compte, un ensemble de points formant une trajectoire proche de la trajectoire théorique d'un signal parfait (c'est-à-dire une sinusoïde, dans notre exemple). Or, cet objectif n'est pas conforme à ce que nous souhaitons, car il met la mémoire ``hors-jeu''. De plus, l'idée même que certains scenarii soient plus valides que d'autres remet en cause le coté binaire du processus d'élagage (tous les scenarii validés sont de même qualité ``bonne'' alors que les scenarii invalidés possèdent une qualité ``mauvaise'').
Admettons que nous souhaitions donner une réponse à ces deux questions. Nous avons remarqué qu'à un instant t, un intervalle élémentaire peut être sélectionné par plusieurs scenarii (paragraphe 3.1.5). Si, pour cet instant t, nous comptons pour chaque intervalle élémentaire le nombre de sélections, nous pouvons établir une courbe analogue à celle d'une densité de probabilité de présence du signal à l'instant t (figure 3.9, en haut). À partir de ces données, on peut déterminer la valeur du signal reconstruit en utilisant une probabilité de choix dépendant du nombre de sélection de chacun des intervalles élémentaires (voir l'algorithme 3.2 ). Le signal reconstruit peut ainsi être réinjecté au processus d'élagage. La figure 3.9 montre que le signal d'origine est sensiblement amélioré par cette méthode; en particulier, les points pris aléatoirement (figures de droite) sont éliminés dès la première itération. De plus, il faut noter qu'au bout de deux ou trois itérations de l'algorithme de bouclage, il n'existe plus de différence de ``qualité'' entre deux reconstitutions successives. Toutefois, la ``forme'' du signal après ce bouclage peut être relativement différente de celle du signal sinusoïdal théorique (figure en bas à droite). Cette constatation confirme nos craintes évoquées plus haut: tout comme les données perceptives brutes, les données reconstruites ne peuvent pas être utilisées dans un processus visant à discriminer plusieurs catégories de signaux suivant leur ``forme'' spécifique, avec une quasi-certitude. Cette discrimination doit être effectuée à l'aide du processus d'anticipation, que nous n'avons pas fait intervenir dans ces expériences ( UP_init(t) est égal à l'univers des possibilités total à chaque instant t).

Figure 3.9: Exemples d'application du bouclage.

À partir d'un même signal sinusoïdal, nous appliquons un bruit gaussien ( $\sigma$ = 0.10) d'une part (figures de gauche) et, d'autre part (figures de droite), nous remplaçons la valeur du signal théorique par une valeur aléatoire suivant une loi U[0,1], selon une probabilité $\tau$ = 0.3 (1 point sur 3 en moyenne est choisi au hasard).
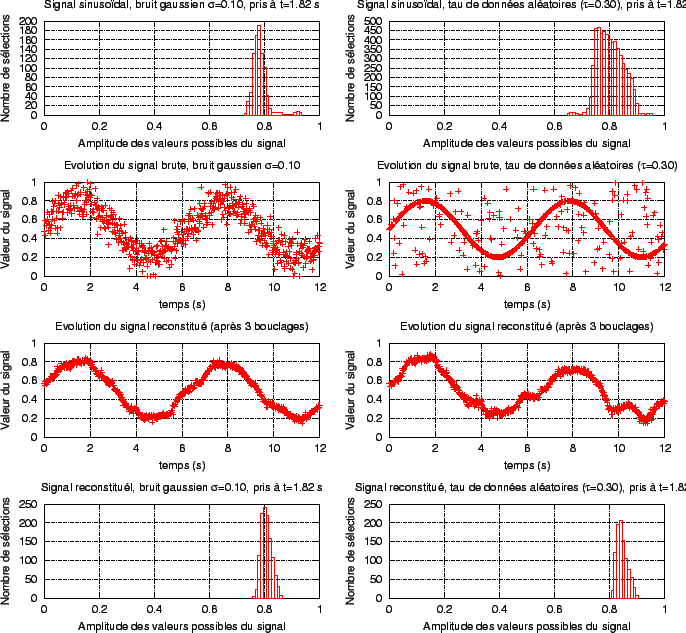
Le procédé de reconstruction du signal explicité dans le paragraphe 3.1.5 considère qu'à chaque instant t, la valeur du signal peut être dans chacun des intervalles élémentaires touchés par au moins un scenario. Les deux figures du haut montrent que, bien que l'étalement des valeurs possibles (à l'instant t=1.82 s) soit important, il existe un pic relativement étroit, montrant que certains intervalles élémentaires sont beaucoup plus sélectionnés que d'autres au cours du temps, pour cet instant précis (t=1.82 s). À l'issue de trois itérations de l'algorithme de bouclage, nous nous apercevons que l'étalement des valeurs possibles est plus étroit (figures du bas), toujours pour l'instant t=1.82 s. Par contre, le signal reconstitué peut être déformé par rapport au signal théorique (figures de droite).

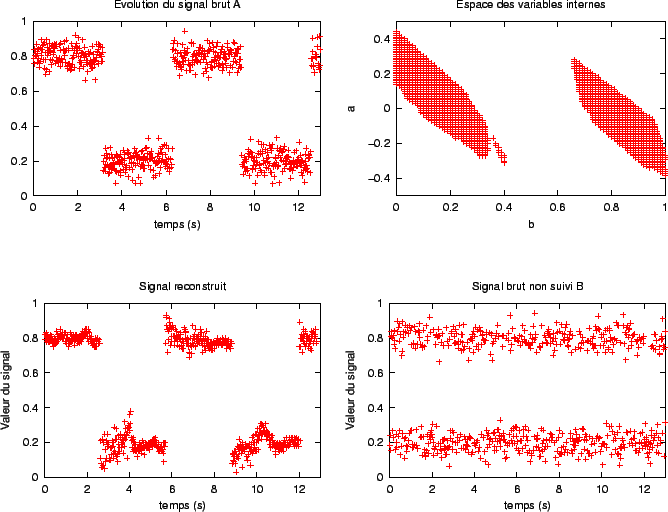
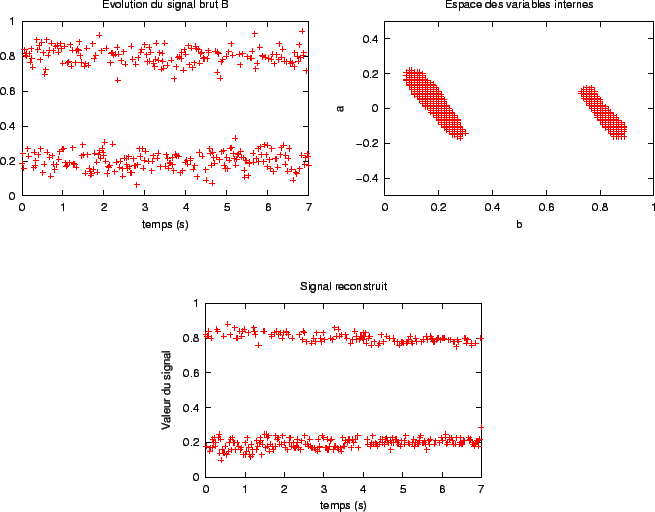
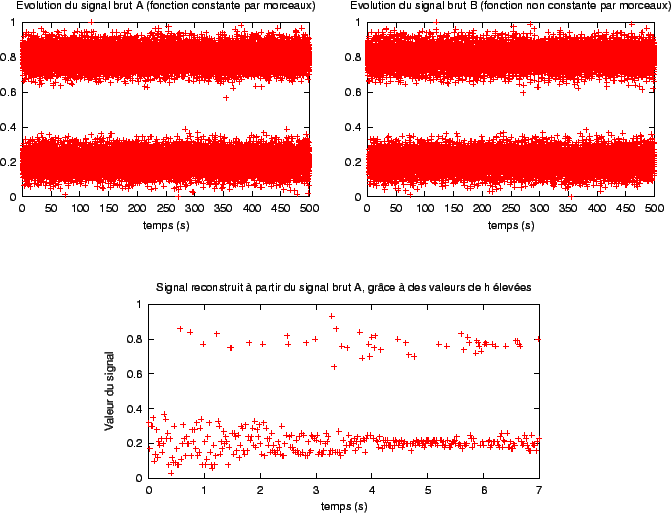
Abordons à présent la troisième expérience préliminaire, donnant les limites de notre algorithme de choix de h (algorithme 2.3, page ). Nous avions déjà mis en évidence certaines limitations (conclusion du chapitre 2). Cependant, l'algorithme d'élagage développé dans le chapitre précédent (algorithme 2.1, page ) n'était pas assez général pour constater d'autres limitations. En particulier, celui-ci ne pouvait pas suivre un signal ``discontinu''. L'exemple donné par la figure 3.10 montre que l'algorithme présenté dans ce chapitre peut suivre de tels signaux, mais sous certaines restrictions, qui dépendent de l'algorithme 2.3. L'exemple qui ``piège'' l'algorithme 2.3 montre un signal construit à partir d'une fonction non continue par morceau. Or, le signal brut ne possède pas une densité de probabilité U[0,1]; l'échec est dû au fait que les valeurs de h imposées par cet algorithme sont trop faibles (on ne prend pas assez de ``hauteur'' pour regarder le signal). En effet, la figure 3.11 montre qu'il est possible de suivre ce signal, en choisissant des valeurs de h plus grandes.

Figure: Mise en oeuvre de l'algorithme d'élagage sur un signal constant par morceaux.

Le signal brut présenté en haut à gauche est obtenu à partir d'un signal théorique périodique et contant par morceaux; un bruit gaussien ( $\sigma$ = 0.05) lui est rajouté. Ce signal produit deux ``tâches'' dans l'espace des variables internes, ce qui correspond à ce que nous attendons. Par contre, le signal présenté en bas à droite ne peut pas être suivi; il est construit en choisissant, à chaque pas de temps, de manière équiprobable, parmi deux valeurs (0.2 et 0.8), puis en rajoutant à la valeur obtenue un bruit gaussien ( $\sigma$ = 0.05). Le non-suivi s'explique facilement: si on considère un tuyau de centre constant dans le temps et égal 0.2 (ou un autre de centre 0.8), il y a statistiquement un point sur deux à l'extérieur de ce tuyau. Or, les valeurs de i utilisées (toujours inférieures à la moitié de la valeur de h) ne permettent pas de répondre à cette contrainte.

Figure: Mise en oeuvre de l'algorithme d'élagage sur un signal non continu par morceaux.

Le signal brut utilisé ici est le même que celui donné en bas à droite de la figure 3.10. L'ensemble des valeurs des couples (h,i) est déterminé en choisissant $\sigma$ = 0.05. L'ordre de priorité du choix des couples est fonction de la largeur l du tuyau. Ceux dont la largeur est la plus faible sont sélectionnés en premier. Ainsi, les valeurs de h sont: 314,256,215,184,160,142. Elles correspondent à des valeurs de l égales à: 0.05,0.06,0.07,0.08,0.09,0.10 .

Les deux derniers signaux bruts étudiés (l'un constant par morceaux et l'autre non continu par morceaux) permettent de donner un bon exemple de l'importance du choix de h dans un problème de discrimination entre deux signaux (problème inclus dans le processus de mémorisation). C'est l'objet de notre dernière expérience préliminaire. Les deux signaux sont construits à partir de fonctions différentes. Pourtant, les occupations de l'espace des variables internes sont très semblables (voir les figures 3.10 et 3.11). En fait, les plages de valeurs touchées sont identiques pour les deux signaux (autour de 0.2 et autour de 0.8), ce qui se traduit par deux ``taches'' centrées autour de b=0.2 et b=0.8 dans l'espace des variables internes. La différence est que dans un cas, ces deux zones de l'espace des variables internes sont activées l'une après l'autre, alors que dans l'autre cas, elles sont activées simultanément. Or, la notion de simultanéité (ou de précédence), qui s'exprime avec une dimension temporelle, semble liée au fait que nous avons l'impression de visualiser deux ou une seule courbe sur les graphiques d'évolution du signal (dimension spatiale). Ainsi, la ``précédence'', constatée pour le signal issu d'une fonction constante par morceaux, dépend de la ``hauteur'' avec laquelle on regarde le signal (donc de la valeur de h). La figure 3.12 montre que si on regarde les deux signaux d'assez haut, on ne peut pas visuellement les différencier. En parallèle, si on reprend le même ensemble des valeurs de h sélectionnées pour traiter le signal dont la fonction n'est pas continue par morceaux, et qu'on l'applique au signal issu d'une fonction constante par morceaux, on constate qu'il n'y a plus de précédence entre zones de l'espace des variables internes activées autour 0.2 et celles activées autour de 0.8 : vu à cette ``hauteur'', ce signal est comparable à celui qui n'est pas continu par morceaux.

Figure: Importance de la valeur de h sélectionnée pour discriminer deux signaux.

Les valeurs de h sélectionnées dans le processus d'élagage, pour le signal A, sont identiques à celles utilisées pour le signal B dans la figure 3.11: 314,256,215,184,160,142. Elles correspondent à des valeurs de l égales à: 0.05,0.06,0.07,0.08,0.09,0.10 . On remarque que, dans ce cas, le signal reconstruit ne fait plus apparaître de précédence entre les instants où les valeurs du signal sont proches de 0.2 et les instants où celles-ci sont proches de 0.8 . La ressemblance entre les signaux A et B dépend donc de la hauteur avec laquelle on regarde les deux signaux (liée aux valeurs de h): cette ressemblance est illustrée par les deux figures du haut, visiblement identiques lorsqu'on regarde l'évolution du signal sur 500 secondes (au lieu de 15 secondes environ dans les exemples précédents).

Ces premières expériences nous permettent de dégager des remarques importantes pour poursuivre notre travail, donnant lieu à une nouvelle proposition spécifiant mieux les contours des processus de perception et de mémorisation:

• l'algorithme d'élagage 3.1 permet de suivre des signaux issus de fonctions non continues par morceaux, ce qui est un progrès par rapport à l'algorithme 2.1 donné dans le chapitre 2.
• la donnée seule de la région ou des régions balayées dans l'espace des variables internes n'est pas suffisante pour distinguer avec certitude un signal d'un autre: la surface totale balayée est souvent importante (deuxième expérience) et deux signaux très différents peuvent aboutir à l'activation de régions presque identiques de l'espace des variables internes.
• dans l'absolu, le signal reconstitué par bouclage interne, même s'il peut être plus précis que le signal brut dans certains cas, ne peut pas être utilisé pour discriminer le signal brut dont il est issu d'autres signaux.
• A priori, il n'est pas possible d'éliminer certains couples (h,i) ou, du moins, d'en privilégier certains par rapport à d'autres (résultat de la dernière expérience). Par conséquent, l'algorithme 2.3 n'est pas valide dans l'absolu, du moins s'il est sorti du contexte donné par le processus de mémorisation, comme c'est le cas jusqu'à présent.

À l'issue de ces expériences préliminaires, nous pouvons spécifier plus précisément le contexte du processus de mémorisation: l'algorithme 2.3, dont le but était de sélectionner h automatiquement, sans avoir recours au processus de mémorisation, a montré ses limites. Cela nous conduit à abandonner cette piste et nous suggère la proposition suivante:

Proposition _s   La sélection de h s'effectue non pas au sein du processus d'élagage, mais dans le processus de mémorisation: il s'agit donc d'une autre variable interne, au même titre que a et b.

Cette proposition sous-entend que la valeur de h ne peut pas être fixée par le processus d'élagage, donc qu'aucune hypothèse sur la valeur de h ne peut être exclue a priori dans celui-ci. D'autre part, comme h est supposée être une variable interne, l'étendue des valeurs possibles de UP_init(t) peut être diminuée par le processus d'anticipation, dépendant du processus de mémorisation. Toutefois, cette modification ne change pas les contraintes existant entre les valeurs de h, i et l; en particulier, l'étendue des valeurs de h admissibles est minorée par un entier dépendant de l.