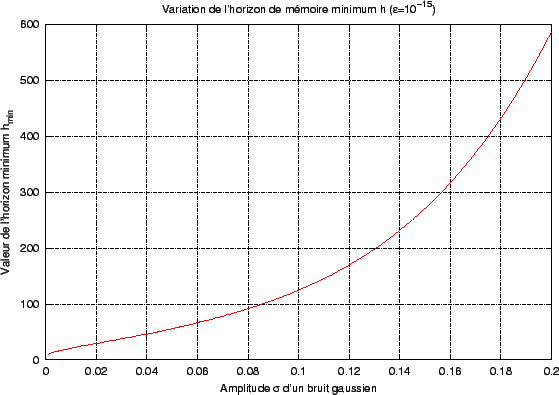
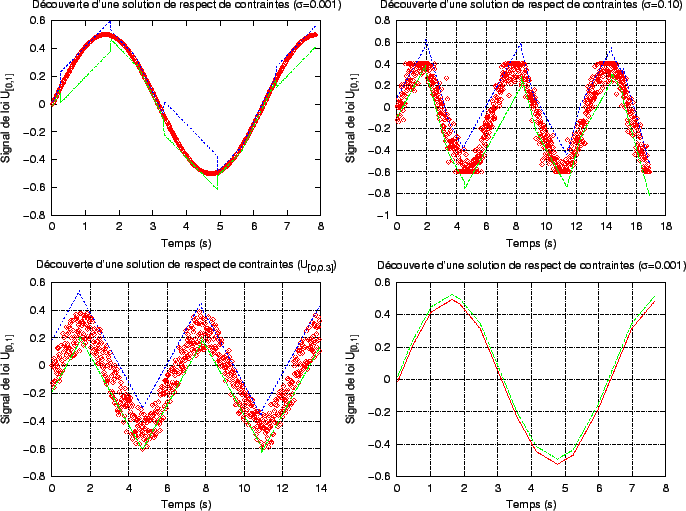
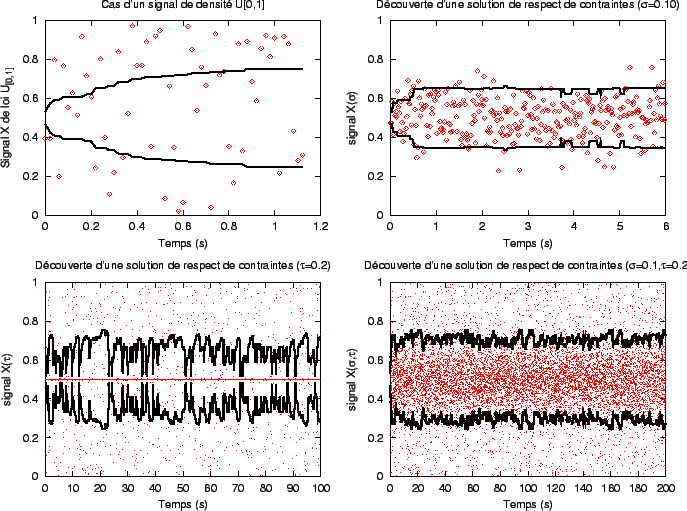
Pour les quatre exemples ci-dessus, le pas de temps entre deux mesures est fixé à 0.02 seconde. La densité FX du signal X est stationnaire et symétrique par rapport à 0.5. Les traits pleins épais correspondent à la limite supérieure du focus (au dessus de 0.5) et à la limite inférieure du focus (en dessous de 0.5), qui, lui-même, est centré sur 0.5 (le focus est immobile au cours du temps). Les variations des bornes inférieure et supérieure du focus montrent l'adaptation de la largeur de celui-ci au cours du temps. Dans ces quatre cas, l peut prendre ses valeurs dans l'ensemble fini {0.032,0.06,0.099,0.149, 0.157, 0.182, 0.22, 0.241, 0.297, 0.303, 0.307, 0.333, 0.338, 0.37, 0.389, 0.402, 0.405, 0.424, 0.434, 0.446, 0.458, 0.471, 0.478, 0.507, 0.502, 0.501}, attaché à l'ensemble des valeurs de 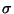 {0.002, 0.005, 0.01, 0.015, 0.02, 0.025, 0.03, 0.035, 0.04, 0.046, 0.051, 0.055, 0.06, 0.065, 0.07, 0.076, 0.08, 0.085, 0.09, 0.095, 0.10, 0.105, 0.11, 0.115, 0.12, 0.125}. {0.002, 0.005, 0.01, 0.015, 0.02, 0.025, 0.03, 0.035, 0.04, 0.046, 0.051, 0.055, 0.06, 0.065, 0.07, 0.076, 0.08, 0.085, 0.09, 0.095, 0.10, 0.105, 0.11, 0.115, 0.12, 0.125}.
Dans le premier cas (figure en haut à gauche), le signal X possède une densité de probabilité U[0,1]. Le temps maximum indiqué correspond à la durée avant l'échec de l'algorithme (pour les valeurs de 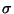 considérées). On remarque l'élargissement progressif du focus au cours du temps, indiquant qu'à aucune étape de l'algorithme, les contraintes n'ont pu être satisfaites. Au contraire, dans le deuxième cas (figure en haut à droite), on applique un signal gaussien de paramètre considérées). On remarque l'élargissement progressif du focus au cours du temps, indiquant qu'à aucune étape de l'algorithme, les contraintes n'ont pu être satisfaites. Au contraire, dans le deuxième cas (figure en haut à droite), on applique un signal gaussien de paramètre
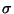 = 0.1;sur la gauche de ce graphe, on remarque la partie transitoire durant laquelle le focus s'élargit progressivement (les 0.7 premières secondes), alors que la partie de droite montre une quasi-stabilité de la largeur du focus. Dans les troisième et quatrième cas (figures du bas), on applique un signal mêlant des valeurs d'un signal de densité gaussienne ( = 0.1;sur la gauche de ce graphe, on remarque la partie transitoire durant laquelle le focus s'élargit progressivement (les 0.7 premières secondes), alors que la partie de droite montre une quasi-stabilité de la largeur du focus. Dans les troisième et quatrième cas (figures du bas), on applique un signal mêlant des valeurs d'un signal de densité gaussienne (
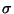 = 0.001 pour la figure de gauche et = 0.001 pour la figure de gauche et
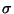 = 0.1 pour la figure de droite) avec un signal de densité U[0,1], apparaissant suivant une fréquence = 0.1 pour la figure de droite) avec un signal de densité U[0,1], apparaissant suivant une fréquence 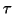 = 0.2. On remarque dans ces deux cas que les bornes du focus oscillent nettement (la règle de choix de l en est ici la cause). = 0.2. On remarque dans ces deux cas que les bornes du focus oscillent nettement (la règle de choix de l en est ici la cause). |
![\begin{algo}
% latex2html id marker 2335
[b]
{\it Initialisation du focus}: L'in...
... focus à une amplitude du bruit gaussien cohérente avec l'expérience.}\end{algo}](img135.gif)