suivant: 3 Idée en vue
monter: 2 Étude du processus
précédent: 1 Point de départ,
Table des matières
2 Conditions à l'obtention d'informations perceptives
Intuitivement, on se rend compte qu'on peut trouver des couples (horizon h de la mémoire, nombre d'erreurs maximum admissible i) pour que la probabilité d'avoir effectivement au moins i erreurs sur h pas de temps soit aussi petite qu'on le souhaite. C'est l'objet de la proposition suivante, dont la preuve est donnée en annexe, page ![[*]](file:/usr/lib/latex2html/icons/crossref.png) .
.
Proposition _s
En admettant que l'ensemble des probabilités
p(
t) définies par la relation
2.8 soit connu pour tout instant t et qu'elles soient minorées par un réel
pmin strictement positif, et qu'on fixe un réel

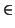
]0, 1], il existe un entier positif
imin tel que, pour tout nombre d'erreurs tolérées i vérifiant
i 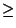 imin
imin, il existe un horizon de mémoire maximum
hmax tel que si un entier h vérifie
hmax 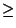 h
h 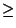 i
i 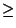 imin
imin, alors la probabilité d'avoir au moins i valeurs du signal en dehors du segment
S sur h pas de temps est inférieure à

, mais cette probabilité est supérieure à

pour
hmax + 1 pas de temps.
Fixons
 > 0. Dans la suite de ce chapitre, nous attribuerons une attention spéciale aux couples (h,i) vérifiant l'hypothèse suivante:
> 0. Dans la suite de ce chapitre, nous attribuerons une attention spéciale aux couples (h,i) vérifiant l'hypothèse suivante:
Hypothèse _s
La probabilité pour que
i valeurs ou plus du signal sortent du segment
S, dont la mémoire a un horizon
h, est inférieure ou égale à

.
D'autre part, comme nous l'avons indiqué au début de ce paragraphe, nous désirons être certains que la découverte d'un ensemble de mouvements appliqués au segment S, permettant de respecter l'hypothèse 11, n'est pas possible si on applique un signal de loi uniforme sur [0,1]. Par là, nous souhaitons nous prémunir contre l'obtention de ``fausses'' informations; ce raisonnement est identique à celui formulé au paragraphe 2.1.4.
Lorsque le signal X(t) suit une loi uniforme sur [0,1], la probabilité pour que le signal touche le segment S de largeur l suit une loi de Bernouilli de paramètre l. La probabilité
Pr(TS = m) suit une loi binomiale de paramètre (h,l) et la probabilité pour que au moins h - i valeurs de X soient dans le tuyau formé par l'évolution de S est donnée par l'expression:
Pr(TS 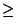 h - i) = h - i) = 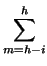 Chmlm Chmlm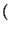 1 - l 1 - l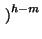 |
(10) |
Lorsque i est fixé, on montre, identiquement à la proposition 1, le fait suivant (voir les annexes, page ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ):
):
Proposition _s
On peut trouver
hmin minimum pour rendre
Pr(
TS 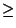 h
h -
i) aussi petit qu'on le souhaite, pour tout
h 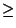 hmin
hmin
D'où la formulation d'une nouvelle hypothèse sur les valeurs de i et h, qui peut être satisfaite pour tout i positif ou nul, sachant qu'on a fixé un
 > 0:
> 0:
Hypothèse _s
La probabilité pour que au moins
h -
i valeurs d'un signal de loi uniforme sur [0,1] soient incluses dans le segment
S de largeur
l est inférieure ou égale à

.
Nous nous intéressons à présent aux couples (h,i) vérifiant à la fois les hypothèses 11 et 12. A priori, il n'est pas évident que ces couples existent pour tout  strictement positif fixé. La proposition suivante, démontrée en annexe, page
strictement positif fixé. La proposition suivante, démontrée en annexe, page ![[*]](file:/usr/lib/latex2html/icons/crossref.png) , donne des conditions d'existence de ces couples.
, donne des conditions d'existence de ces couples.
Proposition _s
Considérons un segment
S de largeur l et supposons que l'ensemble des probabilités
pj soient toutes strictement supérieures à l. Alors, pour tout

> 0, il existe un couple unique
hmin,
i vérifiant à la fois les hypothèses
11 et
12, avec
hmin minimum; c'est-à-dire que pour tout
h <
hmin et pour tout
i <
h au moins une des deux hypothèses
11 ou
12 n'est pas respectée.
D'autre part, si on suppose que l'ensemble des probabilités
pj sont toutes supérieures ou égales à l, alors pour tout

< 0.5, il n'existe aucun couple
h,
i vérifiant simultanément les deux hypothèses
11 et
12.
Pour donner une idée de l'ordre de grandeur de h, nous allons prendre un exemple où on connaît parfaitement FX(t). FX(t) vaut 0 à l'extérieur de [0,1] et vaut
K.e- 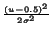 , avec
K =
, avec
K = 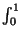 e-
e- 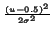 du, sur [0,1]. Si on centre le segment S sur 0.5 (point où la densité de probabilité est maximum), la connaissance de l permet de calculer les pj, qui sont tous égaux dans ce cas (FX est indépendant de t). À partir de cela, nous pouvons déterminer par essais successifs le couple (i,h) tel que
h
du, sur [0,1]. Si on centre le segment S sur 0.5 (point où la densité de probabilité est maximum), la connaissance de l permet de calculer les pj, qui sont tous égaux dans ce cas (FX est indépendant de t). À partir de cela, nous pouvons déterminer par essais successifs le couple (i,h) tel que
h 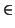 E(
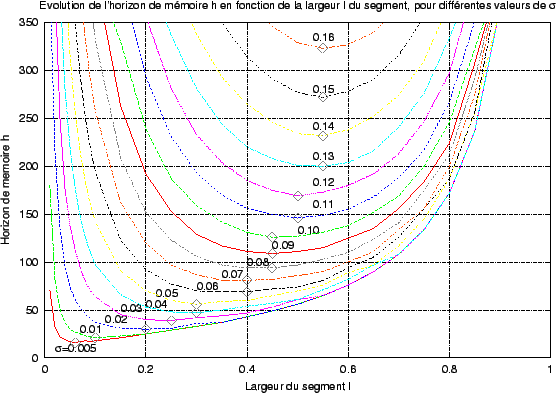
E( , i). La figure 2.19 montre l'évolution de la valeur de h en fonction de l, pour différentes valeurs du paramètre
, i). La figure 2.19 montre l'évolution de la valeur de h en fonction de l, pour différentes valeurs du paramètre 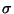 de FX.
de FX.
Cependant, comme nous ne connaissons pas les pj en pratique, le fait de choisir un couple (i, h) en supposant que
h 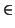 E(
E( , i) conditionne une valeur minimum des pj admissibles. L'expérience permet de confirmer ou d'infirmer cette hypothèse: le fait que l'expérience mette en évidence un cas où i éléments ou plus de la file d'attente soient égaux à ``0'' permet d'infirmer l'hypothèse 11. L'échec possède deux causes possibles:
, i) conditionne une valeur minimum des pj admissibles. L'expérience permet de confirmer ou d'infirmer cette hypothèse: le fait que l'expérience mette en évidence un cas où i éléments ou plus de la file d'attente soient égaux à ``0'' permet d'infirmer l'hypothèse 11. L'échec possède deux causes possibles:
- le positionnement du centre du segment n'est pas adapté (figure 2.20).
- les caractéristiques du segment (l, h, i), conditionnant les pj admissibles, n'est pas adaptée par rapport à l'étalement des densités de probabilité FX(t).
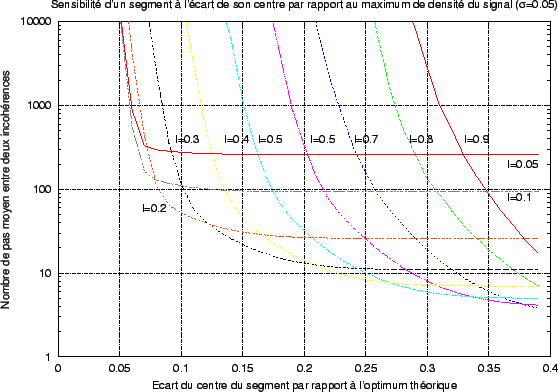
Lorsqu'on définit les caractéristiques d'un segment (l, h, i), on fait une hypothèse sur la nature de FX. Il est intéressant d'avoir une idée de la réponse du segment lorsque celui-ci est mis dans une situation où cette hypothèse n'est pas valide (positionnement du centre ou caractéristiques du segment non adaptés. Les résultats donnés par la figure 2.21, reprenant la densité de probabilité exhibée précédemment, montrent que, pour un segment dont les caractéristiques ont été établies de manière à ``supporter'' une valeur de 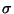 égale à 0.05, la tolérance à l'écart entre le point de densité maximum de FX et la position du centre de S dépend fortement de la largeur de ce dernier. Cependant, à largeur l fixée, la courbe d'évolution du nombre de pas moyens entre deux erreurs montre une caractéristique intéressante: il existe une plage de valeurs de l'écart pour laquelle pratiquement aucune erreur n'est détectée, puis une baisse très marquée du nombre de pas moyen entre deux erreurs, puis enfin une convergence asymptotique vers i + 1; en effet, ce nombre correspond au nombre de pas minimal qu'il faut pour s'apercevoir que les hypothèses ne sont pas respectées. Donc, pour chaque largeur l, il existe un écart ``critique'' à partir duquel le délai pour s'apercevoir du non respect des contraintes se raccourcit fortement. Si on effectue une expérience similaire (avec un segment de mêmes caractéristiques (l,h,i)), mais en faisant varier cette fois-ci la valeur de
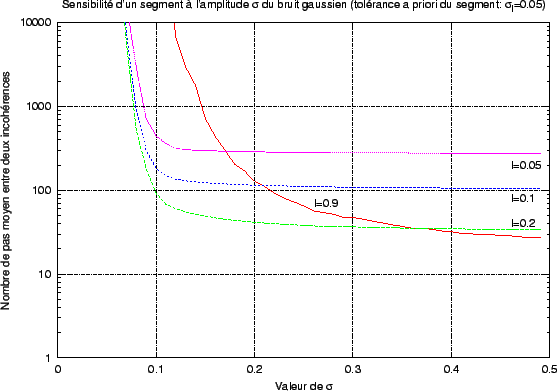
égale à 0.05, la tolérance à l'écart entre le point de densité maximum de FX et la position du centre de S dépend fortement de la largeur de ce dernier. Cependant, à largeur l fixée, la courbe d'évolution du nombre de pas moyens entre deux erreurs montre une caractéristique intéressante: il existe une plage de valeurs de l'écart pour laquelle pratiquement aucune erreur n'est détectée, puis une baisse très marquée du nombre de pas moyen entre deux erreurs, puis enfin une convergence asymptotique vers i + 1; en effet, ce nombre correspond au nombre de pas minimal qu'il faut pour s'apercevoir que les hypothèses ne sont pas respectées. Donc, pour chaque largeur l, il existe un écart ``critique'' à partir duquel le délai pour s'apercevoir du non respect des contraintes se raccourcit fortement. Si on effectue une expérience similaire (avec un segment de mêmes caractéristiques (l,h,i)), mais en faisant varier cette fois-ci la valeur de 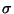 tout en gardant le centre du segment à l'optimum (0.5), on se rend compte d'une évolution similaire du nombre de pas moyen entre deux non-respects des contraintes suivant la largeur du segment (voir la figure 2.22). Les courbes tendent asymptotiquement vers le nombre de pas moyen sans erreur lorsque le signal X possède une densité de probabilité uniforme sur [0,1] (figure 2.23).
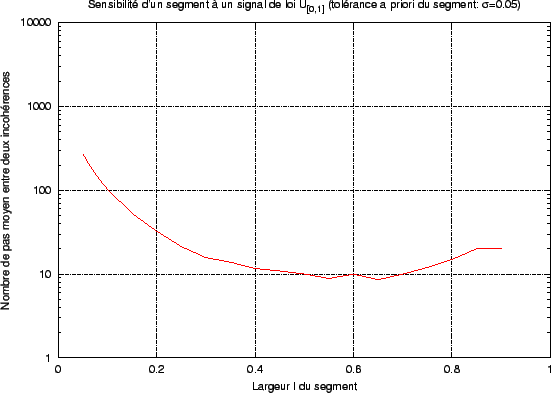
tout en gardant le centre du segment à l'optimum (0.5), on se rend compte d'une évolution similaire du nombre de pas moyen entre deux non-respects des contraintes suivant la largeur du segment (voir la figure 2.22). Les courbes tendent asymptotiquement vers le nombre de pas moyen sans erreur lorsque le signal X possède une densité de probabilité uniforme sur [0,1] (figure 2.23).
Figure:
Exemple d'évolution de l'horizon h de la mémoire suivant la largeur du segment S
Pour cet exemple, on fixe
 = 10-15. Les croix indiquent la position du minimum des courbes, relatives à une valeur particulière de = 10-15. Les croix indiquent la position du minimum des courbes, relatives à une valeur particulière de 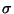 . . |
Figure:
Le segment S est positionné en dehors du maximum de densité de probabilité du signal.
|
|
Figure:
Sensibilité d'un segment à l'écart entre son centre et le point dont la densité est maximum
Le segment S est construit de manière à résister (avec une probabilité
1 -  ) à un signal de densité FX, avec
sigma = 0.05. ) à un signal de densité FX, avec
sigma = 0.05.
 = 10-15. = 10-15. |
Figure:
Sensibilité d'un segment à l'étalement de la densité de probabilité du signal
Le segment S est construit de manière à résister (avec un probabilité
1 -  ) à un signal de densité FX, avec
sigma = 0.05. ) à un signal de densité FX, avec
sigma = 0.05.
 = 10-15. = 10-15. |
Figure:
Sensibilité d'un segment à un signal de loi uniforme sur [0,1]
Le segment S est construit de manière à résister (avec un probabilité
1 -  ) à un signal de densité FX, avec
sigma = 0.05. ) à un signal de densité FX, avec
sigma = 0.05.
 = 10-15. = 10-15. |




suivant: 3 Idée en vue
monter: 2 Étude du processus
précédent: 1 Point de départ,
Table des matières
Frédéric Davesne
2001-07-13
![]() , avec
K =
, avec
K = ![]() e-
e- ![]() du, sur [0,1]. Si on centre le segment S sur 0.5 (point où la densité de probabilité est maximum), la connaissance de l permet de calculer les pj, qui sont tous égaux dans ce cas (FX est indépendant de t). À partir de cela, nous pouvons déterminer par essais successifs le couple (i,h) tel que
h
du, sur [0,1]. Si on centre le segment S sur 0.5 (point où la densité de probabilité est maximum), la connaissance de l permet de calculer les pj, qui sont tous égaux dans ce cas (FX est indépendant de t). À partir de cela, nous pouvons déterminer par essais successifs le couple (i,h) tel que
h ![]() E(
E(![]() , i). La figure 2.19 montre l'évolution de la valeur de h en fonction de l, pour différentes valeurs du paramètre
, i). La figure 2.19 montre l'évolution de la valeur de h en fonction de l, pour différentes valeurs du paramètre ![]() de FX.
de FX.
![]() E(
E(![]() , i) conditionne une valeur minimum des pj admissibles. L'expérience permet de confirmer ou d'infirmer cette hypothèse: le fait que l'expérience mette en évidence un cas où i éléments ou plus de la file d'attente soient égaux à ``0'' permet d'infirmer l'hypothèse 11. L'échec possède deux causes possibles:
, i) conditionne une valeur minimum des pj admissibles. L'expérience permet de confirmer ou d'infirmer cette hypothèse: le fait que l'expérience mette en évidence un cas où i éléments ou plus de la file d'attente soient égaux à ``0'' permet d'infirmer l'hypothèse 11. L'échec possède deux causes possibles: