suivant: 10 Convergence de l'algorithme monter: 5 Conclusion et perspectives précédent: 8 Preuve de la Table des matières

9 Preuve de la proposition 3 (paragraphe 2.2.2, page )

Dans ce paragraphe, nous utiliserons des notations identiques à celles employées dans les preuves données au cours des paragraphes B.3 et B.4, en particulier pour les suites (u_{h, i}), (u^'_{h, i}) et v_{h, m}.
Dans un premier temps, nous allons considérer que les p_j sont tous égaux et valent p. Afin de mieux comprendre la démonstration qui suit, la figure B.4 montre l'évolution des suites u_{h, i} et u^'_{h, i} suivant i, lorsque h est fixé, pour les trois cas de figure suivants:

l < p : cas où il existe des couples solution h, i pour tout $\epsilon$ > 0.
l = p : cas lié, entre autres, au fait de recevoir un signal X(t) dont la densité de probabilité suit une loi uniforme sur [0,1], pour lequel il n'existe pas de couples solution.
l > p : cas lié, entre autres, au fait que le centre du segment S est trop éloigné du point de densité maximale de X(t).

Le plan de notre démonstration est le suivant:

Étude de l'évolution de v_{h, m} suivant m, à h fixé.
Étude du cas l < p: on déduit du point précédent deux fonctions majorantes (une pour u_{h, i} et une pour u^'_{h, i}), qui tendent toutes les deux vers 0 lorsque h tend vers l'infini.
Étude du cas l = p: on montre que u_{h, i} + u^'_{h, i} = 1 pour tout h et tout i.
Étude du cas l > p: on montre que u_{h, i} + u^'_{h, i} $\geq$ 1 pour tout h et tout i $\leq$ h.

$\begin{texdraw} \drawdim{mm} \move (0 3) \lvec (3 1.5) \lvec (0 0) \lvec (0 3) \writeps {0.0 fp} \end{texdraw}$
Lorsque les p_j sont supposés constants, valant p, la probabilité v_{h, m} s'exprime par une loi binomiale de paramètres (h,m):

v_{h, m} = C_h^mp^m(1 - p)^{h - m}

Au regard de quelques exemples d'évolution de v_{h, m} suivant m (voir la figure B.5), à h fixé, nous nous apercevons que l'élément maximum de cette suite est celui dont la valeur est la plus proche du produit p.h. Nous allons montrer que cette observation est justifiée.
Pour cela, nous utilisons une fonction auxiliaire prolongeant v_{h, m} pour des valeurs non entières de h et m.

f (h, m) = c(h, m)p^m(1 - p)^{h - m}

avec

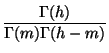c(h, m) = $\displaystyle {\frac{\Gamma(h)}{\Gamma(m) \Gamma(h-m)}}$

La fonction $\Gamma$ d'Euler prolonge la fonction factorielle pour des valeurs non entières.
La dérivée partielle de c(h,m) suivant m est donnée par l'expression suivante:

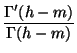$\displaystyle \forall$ h > 0, m $\displaystyle \in$ ]0, h[, $\displaystyle {\frac{\partial c}{\partial m}}$ (h, m) = c(h, m) $\displaystyle \left(\vphantom{ \frac{\Gamma'(h-m)}{\Gamma(h-m)} - \frac{\Gamma'(m)}{\Gamma(m)} }\right.$ $\displaystyle {\frac{\Gamma'(h-m)}{\Gamma(h-m)}}$ - $\displaystyle {\frac{\Gamma'(m)}{\Gamma(m)}}$ $\displaystyle \left.\vphantom{ \frac{\Gamma'(h-m)}{\Gamma(h-m)} - \frac{\Gamma'(m)}{\Gamma(m)} }\right)$

Considérons la fonction d suivante:

$\displaystyle \forall$ m $\displaystyle \in$ [0, h[, d (m) = ln( $\displaystyle \Gamma$ (h - m)) + ln( $\displaystyle \Gamma$ (m))

La fonction d est continue et dérivable sur [1,h]. On remarque que la dérivée d'(m) = - ${\frac{\Gamma'(h-m)}{\Gamma(h-m)}}$ + ${\frac{\Gamma'(m)}{\Gamma(m)}}$ Par conséquent, l'expression de la dérivée partielle de c(h, m) suivant m s'écrit:

$\displaystyle \forall$ h > 0, m $\displaystyle \in$ [0, h[, $\displaystyle {\frac{\partial c}{\partial m}}$ (h, m) = - c(h, m)d'(m)

On en déduit l'expression de la dérivée partielle de f suivant m:

$\displaystyle \forall$ h > 0, m $\displaystyle \in$ [0, h[, $\displaystyle {\frac{\partial f}{\partial m}}$ (h, m) = f (h, m) $\displaystyle \left[\vphantom{ -d'(m) + ln\left(\frac{p}{1-p} \right) }\right.$ - d'(m) + ln $\displaystyle \left(\vphantom{\frac{p}{1-p} }\right.$ $\displaystyle {\frac{p}{1-p}}$ $\displaystyle \left.\vphantom{\frac{p}{1-p} }\right)$ $\displaystyle \left.\vphantom{ -d'(m) + ln\left(\frac{p}{1-p} \right) }\right]$

(20)

Comme f ne s'annule pas, l'annulation de ${\frac{\partial f}{\partial m}}$ (h, m) impose:

- d'(m) + ln $\displaystyle \left(\vphantom{\frac{p}{1-p} }\right.$ $\displaystyle {\frac{p}{1-p}}$ $\displaystyle \left.\vphantom{\frac{p}{1-p} }\right)$ = 0

Nous allons à présent montrer que ce terme s'annule pour une valeur de m ``proche'' de ph. Par construction de $\Gamma$ , on a:

$\displaystyle \Gamma$ (ph + 1) = (ph + 1) $\displaystyle \Gamma$ (ph)
$\displaystyle \Gamma$ (h - ph) = (1 - p)h $\displaystyle \Gamma$ (h - (ph + 1))

Par conséquent:

d (ph + 1) - d (ph) = ln(ph + 1) - ln((1 - p)h)

En mettant p en facteur dans le premier terme de la différence:

d (ph + 1) - d (ph) = ln(p) - ln(1 - p) + ln(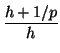 $\displaystyle {\frac{h + 1/p}{h}}$ )

On a donc:

$\displaystyle \forall$ h > 0, d (ph + 1) - d (ph) > ln( $\displaystyle {\frac{p}{1-p}}$ )
lim_h(d (ph + 1) - d (ph)) = ln( $\displaystyle {\frac{p}{1-p}}$ )

On calcule de même:

d (ph) - d (ph - 1) = ln(p) - ln(1 - p) - ln(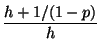 $\displaystyle {\frac{h + 1/(1-p)}{h}}$ )

Par conséquent:

$\displaystyle \forall$ h > 1, d (ph) - d (ph - 1) < ln( $\displaystyle {\frac{p}{1-p}}$ )
lim_h(d (ph) - d (ph - 1)) = ln( $\displaystyle {\frac{p}{1-p}}$ )

Or, d'après le théorème de Rolle, comme d est continue et dérivable sur [0,h[:

$\displaystyle \exists$ m₁ $\displaystyle \in$ [ph, ph + 1], d'(m₁) = d (ph + 1) - d (ph) $\displaystyle \geq$ ln(p) - ln(1 - p)
$\displaystyle \exists$ m₂ $\displaystyle \in$ [ph - 1, ph], d'(m₂) = d (ph) - d (ph - 1) $\displaystyle \leq$ ln(p) - ln(1 - p)

La dérivée d' étant continue, cela signifie que:

$\displaystyle \forall$ h > 1, $\displaystyle \exists$ m₀ $\displaystyle \in$ [ph - 1, ph + 1], d'(m₀) = ln(p) - ln(1 - p)

Ce qui montre que ${\frac{\partial f}{\partial m}}$ (h, m) s'annule sur [ph - 1, ph + 1] pour tout h>1.
D'autre part, ln( $\Gamma$ (m)) étant une fonction convexe deux fois dérivable, sa dérivée seconde est une fonction strictement positive sur [1,h[. De même, la dérivée seconde de ln( $\Gamma$ (h - m)) est strictement positive sur [1,h[ (par composition des fonctions $\Gamma$ (m) et h - m). Par conséquent, d' est croissante sur [1,h[. En particulier, on en déduit que d' ne prend la valeur ln(p) - ln(1 - p) qu'une seule fois, donc, en revenant à l'équation B.4:

${\frac{\partial f}{\partial m}}$ (h, m) ne s'annule qu'une seule fois, dans l'intervalle [ph - 1, ph + 1].
d' étant croissante sur [1,h[ et f positive, on en déduit que le point d'annulation de la dérivée partielle de f est un maximum (dérivée partielle positive sur [1,ph-1] et négative sur [ph+1,h[.

Ce qui conclut le premier point de la preuve.
Nous allons à présent étudier le comportement conjoint des suites (u_{h, i}) et (u^'_{h, i}) suivant les trois cas évoqués au début de ce paragraphe.
Dans un premier temps, nous considérons l'hypothèse l < p. Le travail effectué dans le premier point nous permet d'écrire l'inégalité suivante, pour tout k_p < [ph]:

$\displaystyle \forall$ k $\displaystyle \leq$ k_p, C_h^kp^k(1 - p)^{h - k} $\displaystyle \leq$ C_h^k_pp^k_p(1 - p)^{h - k_p}

(21)

De même, pour tout k_l > [lh] + 1:

$\displaystyle \forall$ k $\displaystyle \geq$ k_l, C_h^kl^k(1 - l )^{h - k} $\displaystyle \leq$ C_h^k_lp^k_l(1 - l )^{h - k_l}

(22)

Par conséquent, en sommant suivant différentes valeurs de k, on obtient:

$\displaystyle \sum_{k=0}^{k_{p}}$ C_h^kp^k(1 - p)^{h - k} $\displaystyle \leq$ (k_p + 1)C_h^k_pp^k_p(1 - p)^{h - k_p}	(23)
$\displaystyle \sum_{k=k_{l}}^{h}$ C_h^kl^k(1 - l )^{h - k} $\displaystyle \leq$ (h - k_l + 1)C_h^k_ll^k_l(1 - l )^{h - k_l}	(24)

Or, pour tout p et tout l vérifiant p > l, on a la relation suivante:

$\displaystyle \exists$ h₀, $\displaystyle \forall$ h > h₀, $\displaystyle \exists$ k_*, [lh] + 1 < k_* < [ph]

Par conséquent, k_* vérifie simultanément les relations B.5 et B.6. Or, si on pose k_* = h - i_*, avec i_* $\in$ [(1 - p)h,(1 - l )h], les deux sommes précédentes ne sont autres que u_{h, i_*} et u^'_{h, i_*}. D'où les relations suivantes, vérifiées simultanément par i_*:

u_{h, i_} $\displaystyle \leq$ (h - i_ + 1)C_h^i_p^{h - i_}(1 - p)^i_*
u^'_{h, i_} $\displaystyle \leq$ (i_ + 1)C_h^i_l^{h - i_}(1 - l )^i_*

Pour montrer que les deux majorants des relations B.5 et B.6 tendent vers 0, nous allons rechercher un équivalent de ceux-ci lorsque h tend vers l'infini. D'après la formule de Stirling, un équivalent de n! est:

n! $\displaystyle \underset{h \rightarrow \infty}\sim$ $\displaystyle \sqrt{2 \pi}$ n $\displaystyle \left(\vphantom{\frac{n}{e} }\right.$ $\displaystyle {\frac{n}{e}}$ $\displaystyle \left.\vphantom{\frac{n}{e} }\right)^{n}_{}$

Nous remarquons que lorsque h devient grand, i_* devient grand, car i_* $\geq$ (1 - p)h. Par conséquent, l'équivalent précédent s'applique aux trois factorielles de C_h^i_*. On peut donc donner un équivalent du majorant de u_{h, i_*} et de celui de u^'_{h, i_*}.

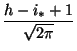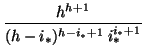(h - i_* + 1)C_h^i_p^{h - i_}(1 - p)^i_* $\displaystyle \underset{h \rightarrow \infty}\sim$ $\displaystyle {\frac{h - i_{} + 1}{\sqrt{2 \pi}}}$ $\displaystyle {\frac{h^{h+1}}{(h - i_{})^{h - i_{}+1} \: i_{}^{i_{} + 1}}}$ p^{h - i_}(1 - p)^i_*
(i_* + 1)C_h^i_l^{h - i_}(1 - l )^i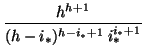_* $\displaystyle \underset{h \rightarrow \infty}\sim$ $\displaystyle {\frac{i_{} + 1}{\sqrt{2 \pi}}}$ $\displaystyle {\frac{h^{h+1}}{(h - i_{})^{h - i_{}+1} \: i_{}^{i_{} + 1}}}$ l^{h - i_}(1 - l )^i_*

En posant i_* = $\alpha$ h, avec $\alpha$ $\in$ [1 - p, 1 - l], les équivalents précédents s'écrivent:

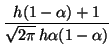$\displaystyle {\frac{h(1-\alpha) + 1}{\sqrt{2 \pi} \: h \alpha (1 - \alpha)}}$ g_p(h, $\displaystyle \alpha$ )
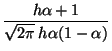$\displaystyle {\frac{h \alpha + 1}{\sqrt{2 \pi} \: h \alpha (1 - \alpha)}}$ g_l(h, $\displaystyle \alpha$ )

avec:

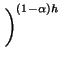g_p(h, $\displaystyle \alpha$ ) = $\displaystyle \left(\vphantom{\frac{p}{1 - \alpha}}\right.$ $\displaystyle {\frac{p}{1 - \alpha}}$ $\displaystyle \left.\vphantom{\frac{p}{1 - \alpha}}\right)^{(1-\alpha)h}_{}$ $\displaystyle \left(\vphantom{ \frac{1-p}{\alpha} }\right.$ $\displaystyle {\frac{1-p}{\alpha}}$ $\displaystyle \left.\vphantom{ \frac{1-p}{\alpha} }\right)^{\alpha h}_{}$
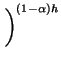g_l(h, $\displaystyle \alpha$ ) = $\displaystyle \left(\vphantom{\frac{l}{1 - \alpha}}\right.$ $\displaystyle {\frac{l}{1 - \alpha}}$ $\displaystyle \left.\vphantom{\frac{l}{1 - \alpha}}\right)^{(1-\alpha)h}_{}$ $\displaystyle \left(\vphantom{ \frac{1-l}{\alpha} }\right.$ $\displaystyle {\frac{1-l}{\alpha}}$ $\displaystyle \left.\vphantom{ \frac{1-l}{\alpha} }\right)^{\alpha h}_{}$

Montrons que à présent que g_p(h, $\alpha$ ) et g_l(h, $\alpha$ ) deviennent conjointement aussi petits qu'on le souhaite. Pour cela, considérons ln(g_p(h, $\alpha$ )) et ln(g_l(h, $\alpha$ ):

ln(g_p(h, $\displaystyle \alpha$ )) = hq_p( $\displaystyle \alpha$ ) avec q_p( $\displaystyle \alpha$ ) = (1 - $\displaystyle \alpha$ )ln( $\displaystyle {\frac{p}{1 - \alpha}}$ ) + $\displaystyle \alpha$ ln( $\displaystyle {\frac{1-p}{\alpha}}$ )
ln(g_l(h, $\displaystyle \alpha$ )) = hq_l( $\displaystyle \alpha$ ) avec q_l( $\displaystyle \alpha$ ) = (1 - $\displaystyle \alpha$ )ln( $\displaystyle {\frac{l}{1 - \alpha}}$ ) + $\displaystyle \alpha$ ln( $\displaystyle {\frac{1-l}{\alpha}}$ )

Les variations de q_p( $\alpha$ ) et de q_l( $\alpha$ ) sont données à partir de leur dérivée:

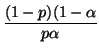q^'_p( $\displaystyle \alpha$ ) = ln( $\displaystyle {\frac{(1-p)(1 - \alpha}{p \alpha}}$ )
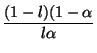q^'_l( $\displaystyle \alpha$ ) = ln( $\displaystyle {\frac{(1-l)(1 - \alpha}{l \alpha}}$ )

Or, si $\alpha$ $\in$ [1 - p, 1 - l], des encadrements montrent que q^'_p(x) $\leq$ 0 et q^'_l(x) $\geq$ 0 pour x $\in$ [1 - p, 1 - l]. Par conséquent, q_p(x) $\leq$ q_p(1 - p) et q_l(x) $\leq$ q_l(1 - l ). Or, q_p(1 - p) = q_l(1 - l )= 0.
Par conséquent, pour $\alpha$ $\in$ ]1 - p, 1 - l[, on a les deux inégalités q_p( $\alpha$ ) < 0 et q_l( $\alpha$ ) < 0 , simultanément, indépendamment de h. Ce qui montre que:

$\displaystyle \lim_{h \rightarrow \infty}^{}$ ln(g_p(h, $\displaystyle \alpha$ )) = - $\displaystyle \infty$
$\displaystyle \lim_{h \rightarrow \infty}^{}$ ln(g_l(h, $\displaystyle \alpha$ )) = - $\displaystyle \infty$

Par conséquent:

$\displaystyle \lim_{h \rightarrow \infty}^{}$ g_p(h, $\displaystyle \alpha$ ) = 0
$\displaystyle \lim_{h \rightarrow \infty}^{}$ g_l(h, $\displaystyle \alpha$ ) = 0

Comme:

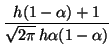$\displaystyle \lim_{h \rightarrow \infty}^{}$ $\displaystyle {\frac{h(1-\alpha) + 1}{\sqrt{2 \pi} \: h \alpha (1 - \alpha)}}$ = $\displaystyle {\frac{1}{\sqrt{2 \pi} \: \alpha}}$ > 0
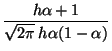$\displaystyle \lim_{h \rightarrow \infty}^{}$ $\displaystyle {\frac{h \alpha + 1}{\sqrt{2 \pi} \: h \alpha (1 - \alpha)}}$ = $\displaystyle {\frac{1}{\sqrt{2 \pi} \: (1 - \alpha)}}$ > 0

On en déduit que les fonctions majorantes de (u_{h, i}) et de (u^'_{h, i}) peuvent être rendues simultanément aussi petites qu'on le souhaite, en fixant un i dans l'intervalle ]lh, ph[. Comme ces suites sont positives par définition (probabilités), nous venons donc de démontrer le premier cas de figure p>l (l'existence d'un h_min unique tel que défini dans la proposition initiale est triviale: c'est la borne inférieure des solutions (h,i(h)) vérifiant les deux hypothèses 11 et 12).
Dans le cas de figure l=p, il suffit de reprendre les relations de récurrence concernant (u_{h, i}) et (u^'_{h, i}) pour constater directement que u_{h, i}u^'_{h, i} = 1 pour tout h et tout i $\leq$ h. Par conséquent, u_{h, i} et u^'_{h, i} ne peuvent pas être simultanément inférieurs à 0.5. Donc, pour tout $\epsilon$ < 0.5, il n'existe aucun couple de solutions (h,i) vérifiant les deux hypothèses.
Considérons à présent le dernier cas de figure (l>p). Soit (S_{h, i}) la suite définie par:

$\displaystyle \forall$ h $\displaystyle \in$ $\displaystyle \mathbb {N}$ , $\displaystyle \forall$ i $\displaystyle \in$ $\displaystyle \mathbb {N}$ , i $\displaystyle \leq$ h, S_{h, i} = u_{h, i} + u^'_{h, i})

Nous allons montrer par récurrence sur h que chaque terme S_{h, i} est supérieur ou égal à 1.
Pour h=1, S_{1, 0} = 1 et S_{1, 1} = (1 - p) + l > 1. L'hypothèse de récurrence est donc vraie pour h=1.
Supposons que cette hypothèse soit vraie jusqu'au rang h $\geq$ 1. Posons l = p + $\alpha$ , avec $\alpha$ > 0. Nous allons déterminer une relation de récurrence liant les S_{h, i}. Pour cela, nous utilisons celles existant entre les u_{h, i} et entre les u^'_{h, i} permettent d'écrire:

u_{h + 1, i + 1} + u^'_{h + 1, i + 1} = (1 - p)u_{h, i} + p.u_{h, i + 1} + (1 - p - $\displaystyle \alpha$ )u^'_{h, i} + (p + $\displaystyle \alpha$ )u^'_{h, i + 1}

En regroupant les termes, il vient:

S_{h + 1, i + 1} = (1 - p)S_{h, i} + p.S_{h, i + 1} + $\displaystyle \alpha$ (u^'_{h, i + 1} - u^'_{h, i})

Or, u^'_{h, i + 1} - u^'_{h, i} = v^'_{h, i + 1} $\geq$ 0. Par conséquent, on a l'inégalité suivante:

S_{h + 1, i + 1} $\displaystyle \geq$ (1 - p)S_{h, i} + p.S_{h, i + 1}

Par hypothèse de récurrence, S_{h, i} $\geq$ 1 et S_{h, i + 1} $\geq$ 1. On en déduit que (1 - p)S_{h, i} + p.S_{h, i + 1} $\geq$ 1 (relation barycentrique). D'où S_{h + 1, i + 1} $\geq$ 1. Cela étant vrai pour tout i $\in$ {0,..., h}, et sachant que S_{h + 1, 0} = 1 $\geq$ 1, on en déduit que $\forall$ i $\in$ {0,.., h + 1}, S_{h + 1, i} $\geq$ 1. Ce qui termine la récurrence.
Nous venons donc de prouver le cas l>p. En effet, la somme de deux termes étant supérieure ou égale à 1, l'un des deux termes doit être supérieur ou égal à 0.5 .
$\begin{texdraw} \drawdim{mm} \move (0 1.5) \lvec (3 3) \lvec (3 0) \lvec (0 1.5) \writeps {0.0 fp} \end{texdraw}$

**Figure:** Une idée de l'évolution des probabilités u et u' suivant i.
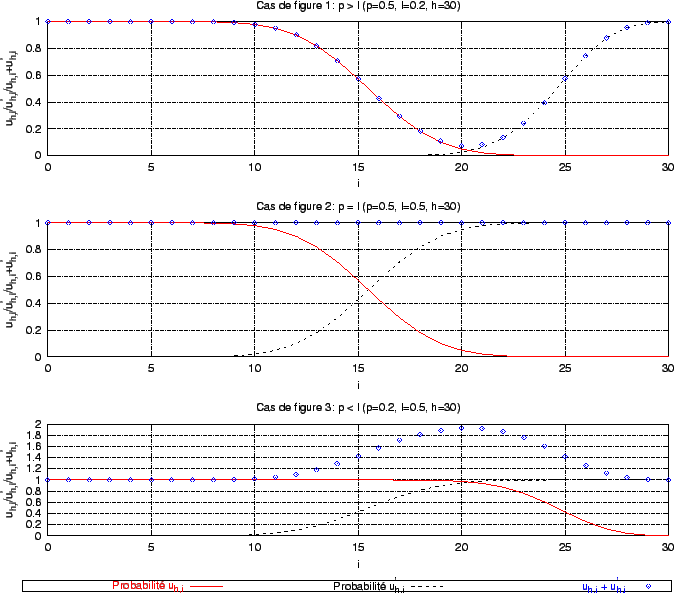
$\includegraphics{fig/trois_cas.eps}$ La somme u_{h, i} + u^'_{h, i} représente la propension des deux suites à pouvoir ou non avoir des valeurs petites simultanément.

**Figure:** Évolution de la suite v, suivant m, à h fixé.
$\includegraphics{fig/v_h_m.eps}$

Éléments relatifs au chapitre 4

suivant: 10 Convergence de l'algorithme monter: 5 Conclusion et perspectives précédent: 8 Preuve de la Table des matières

Frédéric Davesne 2001-07-13