



suivant: Bibliographie
monter: 5 Conclusion et perspectives
précédent: 9 Preuve de la
Table des matières
10 Convergence de l'algorithme de respect de contraintes
Pour les notations et l'énoncé du problème, se reporter au paragraphe 4.1.4. En particulier, nous faisons référence à l'algorithme 4.1.
Soit S, la somme des marquages de l'ensemble des états perceptifs et des états transitoires. Par hypothèse de construction, S vaut 0 au début de l'apprentissage.
Considérons à présent la valeur de S à l'instant t, notée S(t), et supposons qu'une nouvelle transition est découverte à cet instant. Admettons que cette transition relie l'état transitoire ek, j à l'état perceptif ef.
Deux cas se présentent:
-
Mk, j
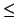 Mf
Mf
-
Mk, j > Mf
Dans le premier cas, l'ajout de cette transition ne modifie pas la cohérence au niveau de ek, j et la phase de propagation n'est pas enclenchée. En outre S reste inchangée.
Le second cas n'est possible que si Mf vaut -1 et Mk, j vaut 0. L'ensemble des états étant cohérent avant l'ajout de la transition, on en déduit que Mk = 0. Mais, dans ce cas, la cohérence est rompue au niveau du noeud ek, j. D'après l'algorithme 4.1, la valeur de Mk, j est fixée en conséquence à -1. Là encore, il existe deux cas de figure:
- il existe un état transitoire ek, j' tel que
Mk, j' = 0
- il n'en existe pas
Dans le premier cas, la phase de propagation se termine, avec
S(t + 1) < S(t).
Dans le second cas, la valeur de Mk est incohérente, et doit être fixée à -1, alors qu'elle valait 0 jusqu'à présent. Il faut alors considérer l'ensemble des états transitoires connectés à Mk et réitérer, pour chacun d'entre-eux, les considérations que nous avons évoquées dans le cas où une nouvelle transition apparaît. Or, nous constatons qu'à chaque itération de la phase de propagation S décroît (cas de continuation de la propagation) ou S reste inchangée (cas d'arrêt d'une branche de la phase de propagation).
La question posée ``La phase de propagation s'arrête-t-elle ?'' trouve alors une réponse. En effet, si nous étudions la suite des valeurs que S prend au cours de la phase de propagation, on constate que S décroît strictement lorsque cette phase trouve un prolongement à un autre noeud. Comme S est minorée par -n.(j+1) 44, on en déduit que la suite (S) converge, ce qui signifie que la phase de propagation s'arrête. Au pire, tous les états sont marqués à -1, ce qui est une situation de cohérence. Dans tous les cas, à la fin de la phase de propagation, le graphe est cohérent (chaque étape de la phase de propagation est une mise en cohérence locale, pour un noeud).
En fait, nous avons également répondu à la question ``L'algorithme converge-t-il ?''. En effet, nous venons de montrer que S(t) est décroissante dans le temps et minorée. Donc, S(t) converge.




suivant: Bibliographie
monter: 5 Conclusion et perspectives
précédent: 9 Preuve de la
Table des matières
Frédéric Davesne
2001-07-13