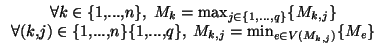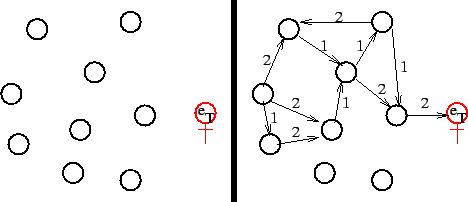
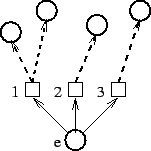
4 Détermination de la valeur de marquage de chaque noeud - loi de cohérence

À partir de la modélisation effectuée dans le paragraphe 4.1.3, nous allons nous inspirer de l'algorithme minimax, afin de déterminer la valeur des marquages associés à chaque état, en fonction des transitions existantes. Le marquage est étendu à l'ensemble des états (ce qui inclus les états transitoires). Voici l'énoncé de la loi de cohérence, valable pour chaque pas de temps, qui donne le marquage M_k de chaque état perceptif e_k ainsi que le marquage M_{k, j} de chaque état transitoire e_{k, j}:

$$\left\{\vphantom{ \begin{array}{c} \forall k \in \{1,...,n\},\:\:... ... \{1,...,q\},\:\:M_{k,j} = \min_{e \in V(M_{k,j})}\{M_{e}\} \end{array}}\right. \begin{array}{c} \forall k \in \{1,...,n\},\:\:M_{k} = \max_{j \i... ...,...,n\} \{1,...,q\},\:\:M_{k,j} = \min_{e \in V(M_{k,j})}\{M_{e}\} \end{array}$$ (16)

Avec V(M_{k, j}) ensemble des indices des états perceptifs vers lesquels une transition issue de l'état transitoire M_{k, j} aboutit. On supposera que si V(M_{k, j}) est vide, alors M_{k, j} vaut 0.
Lorsqu'une nouvelle transition est découverte, nous appliquons l'algorithme 4.1, s'appuyant sur l'équation 4.1, de manière à conserver la cohérence entre les valeurs des marquages associés aux sommets du graphe. Cet algorithme se charge de propager un changement éventuel du marquage d'un noeud à ses voisins.
Pour clore l'algorithme d'apprentissage, il nous faut donner une technique de choix de l'action. Pour cela, si le système est dans un état e_k, nous choisirons en priorité une action a_j dont le marquage M_{k, j} vaut 0. S'il en existe plusieurs, on en choisira une au hasard.
Plusieurs questions méritent d'être posées face à cet algorithme ``simpliste'':

1. la phase de propagation termine-t-elle toujours et rend-elle le graphe cohérent ?
2. l'algorithme converge-t-il ?
3. quelles sont les conditions pour que, s'il existe une solution au problème de respect de contraintes (compte tenu de la spécification des états), l'algorithme la trouve ?

La réponse aux deux premières question est ``oui''. Les preuves sont données en annexes, dans le paragraphe C.1.
La réponse à la troisième question est plus complexe. Une condition suffisante est triviale: il suffit que par chaque état transitoire, il n'existe qu'une unique transition vers un état perceptif.

Figure: L'apprentissage de la dynamique du système est modélisé par l'ajout de transitions.

À gauche, le graphe initial. À droite, l'ensemble des transitions correspond à la découverte d'un passage d'un état à l'autre au cours de l'expérience de l'entité. Dans cet exemple, nous considérons deux actions, ``1'' et ``2''; les transitions marquées à ``1'' signifient qu'elles sont dues à l'action 1.

Figure: États transitoires du système.

Les états perceptifs sont représentés par des cercles, alors que les états transitoires sont représentés par des carrés. Dans cet exemple, le système possède trois actions. À l'instant t, le système est dans l'état e, qui est lié à trois états transitoires (dépendant du choix effectué). Les transitions (en pointillé) sont le résultats des expériences passées du système, liant l'exécution de chacune de ces actions à un certain nombre d'états perceptifs.