|
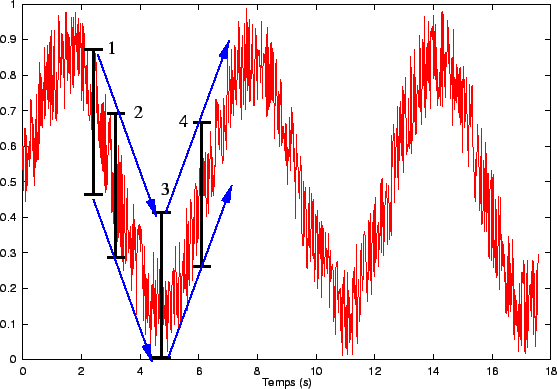
L'évolution du signal suit une fonction sinusoïdale, bruitée artificiellement (loi uniforme d'amplitude 0.3). Sur le graphique, un segment de longueur 0.4 se déplace de la position 1 vers 2 puis 3 avec une vitesse constante. Le mouvement de 3 à 4 résulte d'un changement d'action appliqué à ce segment. |
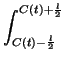 FX(t)(u)du
FX(t)(u)du