4 Essai de mise en pratique: fiabilité des informations perceptives

Dans notre démarche, une information ne peut être utilisée dans le cadre d'un processus décisionnel que si elle est fiable. Ainsi, l'ensemble des données disponibles pour prendre une décision doivent être exactes, ce qui ne signifie pas qu'elles soient précises: notre objectif est de dégager les traits les plus fins possibles d'un signal, en ayant assurance de leur exactitude. Dans ce paragraphe, nous montrons qu'une tendance, prise isolément, n'est pas une information fiable. À partir de ce constat, nous indiquons comment la prise en compte d'informations supplémentaires au cours du temps permet de confirmer ou d'infirmer l'information initiale. En outre, ce processus permet d'éliminer totalement la production d'informations à partir d'un signal aléatoire de probabilité uniforme sur [0,1].
Admettons qu'on détecte un segment orienté. Il est utile de se demander dans quelle proportion cette détection provient d'une réalité observable (le signal traverse réellement ce segment) ou d'un phénomène de ``mirage'' dû au bruit de mesure introduit par le capteur. Pour cela, nous allons considérer un signal aléatoire X régi par une loi uniforme sur [0,1]. Il paraît évident que ce signal ne doit dégager aucune cohérence et qu'on ne peut tirer aucune information fiable à partir de celui-ci. Pourtant, la probabilité Pr de découvrir une information de base (tendance positive ou négative) est non nulle est vaut:

$${\frac{2}{\left(r-1\right)^2}} \geq$$ (1)

Avec Pr⁺ (resp. Pr^-) représentant la probabilité de trouver par hasard une tendance positive (resp. négative) et r représentant la résolution avec laquelle le système P_X perçoit le signal aléatoire. Dans notre cas, r est supérieur ou égal à 3, car le nombre de segments doit être au moins de 3 pour pouvoir détecter une tendance. Cette relation est démontrée en annexe B.1, page et vérifiée par l'expérience dans cette même annexe.
Ce résultat signifie, sans surprise, qu'on ne peut pas se fier à une tendance prise isolément pour une résolution donnée, car la survenue d'une erreur est très probable. Mais, quelles sont les possibilités permettant de réduire ce risque de manière à ce que l'apparition d'une erreur soit théoriquement possible mais pratiquement très improbable ? Car, dans le cas où nous pouvons trouver une méthode permettant de minimiser ce risque de manière à ce qu'une erreur ne surgisse jamais en réalité (même si elle est théoriquement possible), cela signifie que nous sommes capables de spécifier la nature d'informations qui, lorsqu'elles sont détectées, ne peuvent pas être mises en doute (voir le paragraphe 2.1.2).
D'après l'équation 2.1, la probabilité Pr_k⁺ ou Pr_k^- pour que k tendances de même nature (positive ou négative) soient découvertes consécutivement dans le signal aléatoire X est:

$${\frac{1}{\left(r-1\right)^{k+1}}} \geq$$ (2)

De même, la probabilité Pr_k pour que k tendances (quelle que soit leur nature) soient découvertes consécutivement dans le signal aléatoire X est:

$$\left(\vphantom{\frac{2r^{k-1}}{\left(r-1\right)^{2k}}}\right. {\frac{2r^{k-1}}{\left(r-1\right)^{2k}}} \left.\vphantom{\frac{2r^{k-1}}{\left(r-1\right)^{2k}}}\right) \geq$$ (3)

En augmentant k, on peut diminuer les termes Pr_k⁺, Pr_k^- et Pr_k autant qu'on le souhaite. En dessous d'un certain seuil $\epsilon$, on pourra considérer que l'événement n'arrivera jamais en pratique (dans un temps ``raisonnable''). Les équations 2.2 et 2.3 permettent de donner k⁺, k^- et k en fonction de $\epsilon$ et r:

$$\left[\vphantom{-1 - \frac{log(\epsilon)}{log(r-1)} }\right. {\frac{log(\epsilon)}{log(r-1)}} \left.\vphantom{-1 - \frac{log(\epsilon)}{log(r-1)} }\right] \geq$$ (4)

$$\left[\vphantom{ \frac{log(\frac{1}{2}\epsilon r)}{log(\frac{r}{(r-1)^{2}})} }\right. {\frac{log(\frac{1}{2}\epsilon r)}{log(\frac{r}{(r-1)^{2}})}} \left.\vphantom{ \frac{log(\frac{1}{2}\epsilon r)}{log(\frac{r}{(r-1)^{2}})} }\right] \geq$$ (5)

Avec $\left[\vphantom{ }\right.$$\left.\vphantom{ }\right]$ désignant la fonction partie entière et log la fonction logarithme décimal. La table 2.1 donne les valeurs de k, k⁺ et k^- pour $\epsilon$ = 10^-15. La démonstration de ces deux relations est présentée en annexe, page . Dans une partie de ce recueil, nous utiliserons cette valeur arbitraire de $\epsilon$ comme référence. Il est clair que cette valeur seuil détermine le degré de certitude dans le temps de l'information fournie. Pour une durée déterminée, cette valeur conditionne la probabilité pour qu'une erreur survienne, dans la mesure où on connaît le nombre d'informations obtenues dans cet intervalle de temps. Nous discuterons de ce problème dans le paragraphe 2.2.8.
Les tendances sont des briques de base dans la perception du mouvement du signal. On peut les combiner avec des informations concernant la localisation du signal. Si on considère le signal aléatoire X de loi uniforme sur [0,1], la probabilité pour que X(t) appartienne à un segment donné, pour une résolution r, est 1/r. Ainsi, la probabilité Pr_p pour que p valeurs consécutives X(t), X(t + 1),...X(t + p - 1) soient dans ce même segment est:

$$\left(\vphantom{ \frac{1}{r} }\right. {\frac{1}{r}} \left.\vphantom{ \frac{1}{r} }\right)^{p}_{} \geq$$ (6)

Comme précédemment, on peut définir une valeur de p telle que Pr_p soit inférieur ou égal à une probabilité seuil $\epsilon$.

$$\left[\vphantom{ -\frac{log(\epsilon)}{log(r)} }\right. {\frac{log(\epsilon)}{log(r)}} \left.\vphantom{ -\frac{log(\epsilon)}{log(r)} }\right] \geq$$ (7)

La table 2.2 donne les valeurs de p pour $\epsilon$ = 10^-15.
Un regard rapide sur les tables 2.1 et 2.2 nous montre que l'exigence de certitude, telle que nous l'avons définie, aboutit à des valeurs de k, k⁺, k^- et p très élevées, voire même irréalisables pour k⁺ et k^- avec les résolutions 5 et 10. L'expérience montre qu'avec ce degré d'exigence ( $\epsilon$ = 10^-15), aucune tendance ni aucun positionnement statique n'est détecté pour un signal aléatoire de loi uniforme sur [0,1] (se reporter aux annexes, page ).
Appliquons maintenant notre démarche de recherche de cohérence sur un signal Y de la forme Y(t) = $\left(\vphantom{ 1 - \lambda }\right.$1 - $\lambda$$\left.\vphantom{ 1 - \lambda }\right)$f (t) + $\lambda$X(t), avec $\lambda$ $\in$ $\left[\vphantom{0,1}\right.$0, 1$\left.\vphantom{0,1}\right]$ , f (t) = ${\frac{1}{2}}$$\left(\vphantom{ 1 + sin(t) }\right.$1 + sin(t)$\left.\vphantom{ 1 + sin(t) }\right)$ et X(t) signal aléatoire de densité de probabilité uniforme sur [0,1]. Nous constatons que lorsque l'amplitude de l'écart maximum entre deux points consécutifs Y(t) et Y(t + 1) est inférieure strictement à la résolution, la cohérence du signal, à ce niveau de résolution, n'est jamais rompue (tous les points du signal font partie d'une tendance); par contre, le nombre de fois où le signal est déclaré être cohérent décroît très rapidement si cette amplitude devient supérieure à la résolution (voir la figure 2.13). Cette technique a l'avantage de ne produire des informations que pour des résolutions en concordance avec l'amplitude du bruit: les résolutions trop fines par rapport à celui-ci n'expriment quasiment aucune information. Cependant, elle implique une contrainte forte sur la nature du bruit de mesure: celui-ci doit être borné, d'amplitude inférieure à la taille d'un segment (dans notre cas, l'amplitude doit être impérativement inférieure à 0.2). Or, si le bruit de mesure n'est pas borné (bruit gaussien, par exemple), les performances obtenues précédemment s'effondrent. Pour illustrer ce fait, prenons un signal Y défini comme suit:

$\left\{\vphantom{ \begin{array}{c} Y(t)=\frac{1}{2} \left( 1 + sin(t) \right)\... ..., C(t)<\lambda\\ Y(t)=X(t) , si C(t) \geq \lambda\\ \end{array}}\right.$$\begin{array}{c} Y(t)=\frac{1}{2} \left( 1 + sin(t) \right) , si C(t)<\lambda\\ Y(t)=X(t) , si C(t) \geq \lambda\\ \end{array}$

Avec C et X deux variables aléatoires de loi uniforme sur [0,1]. La figure 2.14 montre les résultats obtenus. Nous remarquons que plus la résolution est grossière (r peu élevé), plus les détériorations sont rapides. Cela est dû simplement au fait que plus un segment est grand, plus le nombre de points le touchant est important (suivant la fréquence de rafraîchissement du signal, exprimée par la constante $\tau$ définie au début du paragraphe 2.1.3), donc plus la probabilité d'obtenir une donnée incohérente dans ce segment est élevée.
En conclusion, l'utilisation stricte de l'algorithme de recherche de cohérence permet d'éliminer en pratique les informations ``mirage'' qui pourraient résulter d'un bruit uniforme. Néanmoins, cet algorithme s'avère inadapté pour deux raisons:

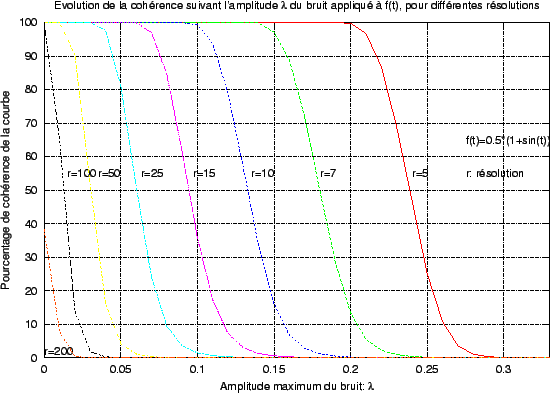
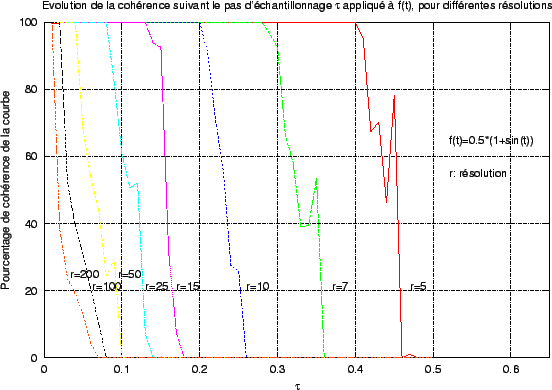
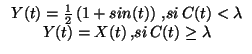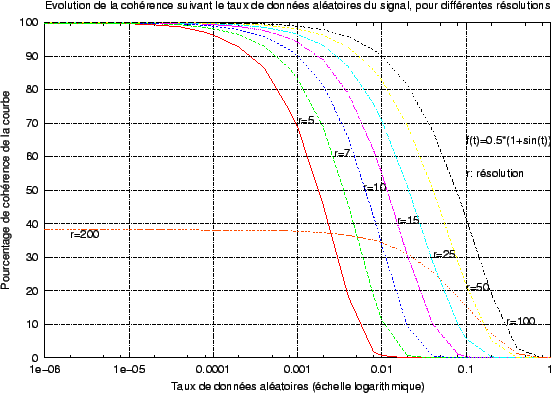
Problème _s   : le nombre de confirmations consécutives est très grand. Par conséquent, lorsque le signal varie rapidement ou lorsque le taux d'échantillonnage est trop faible, le nombre de mesures incluses dans un segment devient trop faible pour apporter une information certaine, puisque le nombre de confirmations nécessaires n'est pas atteint. Le résultat est un ``trou'' dans la suite des informations que notre technique apporte. La figure 2.15 illustre ce fait.

Problème _s   : lorsque l'amplitude maximum du bruit dépasse la taille d'un segment, la cohérence est rompue, même si la probabilité pour que l'écart entre deux mesures dépasse la taille de ce segment est très faible.

Tableau: Valeurs de k, k⁺ et k^- pour $\epsilon$ = 10^-15

Résolution r 5 10 25 50 100

k 29 16 11 9 7

k⁺, k^- 21 15 10 8 7

Les calculs ont été effectués grâce aux équations 2.4 et 2.5.

Tableau: Valeurs de p pour $\epsilon$ = 10^-15

Résolution r 5 10 25 50 100

p 22 16 11 9 8

Les calculs ont été effectués grâce à l'équation 2.8.

Figure: Cohérence détectée en fonction de l'amplitude du bruit de mesure

La fonction artificiellement bruitée par un bruit de loi uniforme d'amplitude $\lambda$ est f (t) = ${\frac{1}{2}}$$\left(\vphantom{ 1 + sin(t) }\right.$1 + sin(t)$\left.\vphantom{ 1 + sin(t) }\right)$.

Figure: Cohérence détectée en fonction du taux de données aléatoires

La fonction est f (t) = ${\frac{1}{2}}$$\left(\vphantom{ 1 + sin(t) }\right.$1 + sin(t)$\left.\vphantom{ 1 + sin(t) }\right)$.

Figure: Cohérence détectée en fonction du taux d'échantillonnage.

La fonction est f (t) = ${\frac{1}{2}}$$\left(\vphantom{ 1 + sin(t) }\right.$1 + sin(t)$\left.\vphantom{ 1 + sin(t) }\right)$. Elle n'a pas été bruitée artificiellement.
On remarque que la cohérence commence à chuter lorsque $\tau$ > 2r. Cela provient du fait que, dans le cas de cette sinusoïde, la différence entre deux mesures est majorée par ${\frac{\tau}{2}}$. Par conséquent, lorsque $\tau$ < 2r, la différence entre deux mesures est inférieure à r, donc la cohérence est préservée: deux mesures consécutives se trouvent soit dans le même segment, soit dans deux segments voisins.