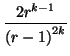suivant: 7 Preuve de la
monter: 5 Conclusion et perspectives
précédent: 5 Probabilité de découverte
Table des matières
6 Découverte de n tendances consécutives pour un signal de densité de probabilité uniforme
Nous allons montrer puis vérifier expérimentalement la relation 2.2, liant la probabilité
Prk+ de découvrir k tendances consécutives de même signe avec cette valeur k, lorsqu'un signal X(t) de densité de probabilité uniforme sur [0,1] est appliqué:
Prk- = 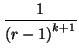 , r , r 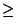 2 + k 2 + k |
|
Nous montrons cette expression par récurrence sur k. Elle est vraie pour k=1 (relation 2.1).
Admettons qu'elle soit vraie pour k > 1. Soit ik+ la tendance positive que nous venons de découvrir ``par hasard''. Or, lorsqu'on a découvert ik+, la probabilité d'en trouver une seconde consécutivement
ik + 1+ se résume à la probabilité de passer de l'état ik + 1 à l'état ik + 2 (en reprenant un graphe similaire à la figure B.2).
En reprenant le même raisonnement que pour la démonstration de l'expression de Pr+ (voir l'annexe B.1), la probabilité de passage de ik + 1 à ik + 2 en un pas de temps est égale à
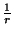 ; pour deux pas de temps, la probabilité est de
; pour deux pas de temps, la probabilité est de
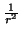 ; pour j pas de temps, la probabilité est de
; pour j pas de temps, la probabilité est de
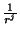 . On en déduit que la probabilité de passage de ik + 1 à ik + 2 s'exprime par la somme infinie suivante:
. On en déduit que la probabilité de passage de ik + 1 à ik + 2 s'exprime par la somme infinie suivante:
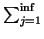
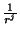 . Or, cette expression est égale à
. Or, cette expression est égale à
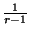 . Par conséquent, la probabilité de détecter k+1 tendances positives consécutives est:
Prk + 1 = Prk.
. Par conséquent, la probabilité de détecter k+1 tendances positives consécutives est:
Prk + 1 = Prk.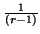 =
= 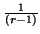 . Cette expression est valable uniquement si l'ensemble des segments ik comporte au moins un élément supplémentaire ik + 2 par rapport au degré de récurrence inférieur. Donc, elle est valable lorsque le nombre de segments est supérieur ou égal à (k+1) + 1. Ce qui termine la récurrence.
. Cette expression est valable uniquement si l'ensemble des segments ik comporte au moins un élément supplémentaire ik + 2 par rapport au degré de récurrence inférieur. Donc, elle est valable lorsque le nombre de segments est supérieur ou égal à (k+1) + 1. Ce qui termine la récurrence.
En ce qui concerne la découverte de k tendances consécutives (quelle que soit la nature des tendances), la probabilité Pr s'exprime par la relation 2.3:
Nous allons montrer cette relation par récurrence.
Constatons qu'elle est vraie pour k=1 (il s'agit la relation 2.1). Admettons qu'elle soit vraie pour k > 1. Considérons la dernière tendance que nous venons de découvrir ``par hasard''. Pour fixer les idées, nous admettrons que celle-ci est positive et se nomme ik+. Or, lorsqu'on a découvert ik+, la probabilité d'en trouver une seconde consécutivement découle de deux cas possibles: on découvre une tendance positive
ik + 1+ ou on découvre une tendance négative ik-. Or, la probabilité d'occurrence du premier cas est
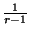 (d'après la démonstration précédente) et la probabilité d'occurrence de la deuxième possibilité est
(d'après la démonstration précédente) et la probabilité d'occurrence de la deuxième possibilité est
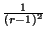 (probabilité de construire une tendance à partir du segment ik + 1 ). Par conséquent, la probabilité de découvrir k+1 tendances ``au hasard'' est donnée par la relation de récurrence:
Prk + 1 = Prk.(
(probabilité de construire une tendance à partir du segment ik + 1 ). Par conséquent, la probabilité de découvrir k+1 tendances ``au hasard'' est donnée par la relation de récurrence:
Prk + 1 = Prk.(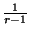 +
+ 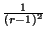 ). Or, par hypothèse de récurrence,
Prk =
). Or, par hypothèse de récurrence,
Prk = 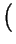
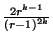
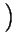 et
et
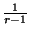 +
+ 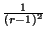 =
= 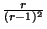 , ce qui donne la relation énoncée au rang k+1. D'autre part, si la nouvelle tendance découverte est positive, on a besoin d'un segment en plus par rapport aux hypothèses du rang k, c'est-à-dire
r
, ce qui donne la relation énoncée au rang k+1. D'autre part, si la nouvelle tendance découverte est positive, on a besoin d'un segment en plus par rapport aux hypothèses du rang k, c'est-à-dire
r 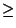 2 + k + 1. Ce qui termine la récurrence.
2 + k + 1. Ce qui termine la récurrence.
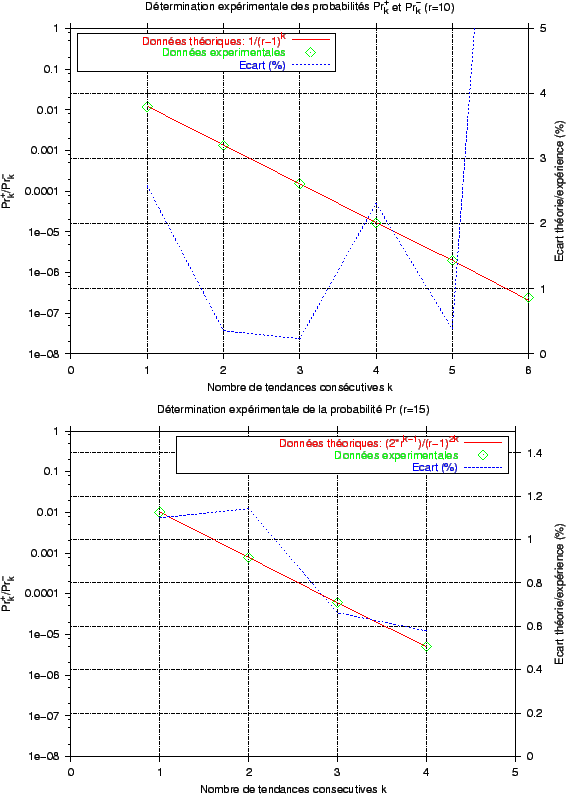
Après avoir effectué ces deux démonstrations, nous allons les confirmer expérimentalement. Pour cela, nous allons utiliser un dispositif expérimental similaire à celui du paragraphe B.1. Pour la confirmation expérimentale de l'expression 2.2, nous allons utiliser une résolution r=10 et nous allons compter le nombre d'itérations de l'algorithme de suivi de cohérence pour que 2000 occurrences de une, deux, trois, quatre et cinq tendances consécutives apparaissent. Nous détectons uniquement des tendances positives en fixant la première valeur du signal X(0) dans le segment i0: cela permet d'éviter les cas où la découverte de n tendances positives consécutives est rendue impossible car le rang du segment touché par X(0) est supérieur à r - k - 2. D'autre part, pour la confirmation expérimentale de 2.3, nous fixons la première valeur du signal X(0) dans le segment médian de [0,1], pour les mêmes raisons que précédemment, et nous utilisons une résolution r=15.
Pour des raisons de temps de calcul, nous limitons à 200 le nombre d'occurrences découvertes de six tendances consécutives.
Les résultats sont rassemblés dans la figure B.3 et confirment la validité des deux relations 2.2 et 2.3.
Si l'on choisit une valeur de n assez grande, on peut donc faire chuter
Prk, Prk+ et
Prk- aussi bas qu'on le souhaite. Pour donner un ordre d'idée, si cette grandeur est de 10-15 (valeur choisie comme référence dans une grande partie du chapitre 2), associée à l'apparition de n tendances consécutives, la probabilité pour que cet événement se produise au bout de p itérations est égale à
1 - (1 - 10-15)p. Pour que cette probabilité soit égale à 0.95, p doit dépasser
1.31015 itérations !
Figure:
Confrontation des résultats théoriques et expérimentaux concernant les expressions Prk et Prk+/-
|
|




suivant: 7 Preuve de la
monter: 5 Conclusion et perspectives
précédent: 5 Probabilité de découverte
Table des matières
Frédéric Davesne
2001-07-13