suivant: 2 Évolution de la
monter: 1 Extension du processus
précédent: 1 Extension du processus
Table des matières
Dans les exemples présentés jusqu'à présent, les actions internes se limitent à donner une trajectoire rectiligne aux tuyaux générés, à partir d'un point initial dont on suppose arbitrairement qu'il est confondu avec C0 (voir l'algorithme 2.1, page ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ). De plus, le nombre d'actions possibles est (très) limité; en outre, nous ne nous sommes pas posé la question de l'influence du choix de cet ensemble initial sur la probabilité réelle d'obtenir une fausse information: nous avons supposé que cette probabilité restait voisine du
). De plus, le nombre d'actions possibles est (très) limité; en outre, nous ne nous sommes pas posé la question de l'influence du choix de cet ensemble initial sur la probabilité réelle d'obtenir une fausse information: nous avons supposé que cette probabilité restait voisine du  à partir duquel nous savons déterminer les caractéristiques h et i d'un focus pris isolément. D'un autre côté, nous avons montré que la ``taille'' de cet ensemble ne doit pas être trop ``grosse'' pour que des signaux aléatoires ne puissent pas être suivis (exemple de la figure 2.26, page
à partir duquel nous savons déterminer les caractéristiques h et i d'un focus pris isolément. D'un autre côté, nous avons montré que la ``taille'' de cet ensemble ne doit pas être trop ``grosse'' pour que des signaux aléatoires ne puissent pas être suivis (exemple de la figure 2.26, page ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
).
L'objectif de ce paragraphe est de préciser ces faits, qui restent vagues pour l'instant. Mais, nous tenons à avertir le lecteur que nous ne fournissons pas ici de preuve théorique de la généralisation des propositions 1 et 3 (voir le paragraphes 2.2.2), bien que des résultats tendent à conforter l'idée que des résultats analogues peuvent effectivement être trouvés. En fait, le calcul exact (ou même le calcul d'un majorant) de la probabilité d'existence d'un tuyau contenant h-i points sur h possibles d'un signal U[0,1] est délicat. Toutefois, cette difficulté ne nous empêche pas de poser le problème.
Dans un premier temps, nous allons agrandir l'ensemble des actions internes générant des trajectoires rectilignes aux focus: nous allons passer d'un ensemble fini à un ensemble infini AR, qui correspondra à toutes les trajectoires rectilignes possibles, entre un instant t et un instant t+d, sur h pas de temps37(voir la figure 3.1). Une trajectoire particulière est caractérisée par deux paramètres a et b, vérifiant les deux équation suivantes:
La deuxième équation impose des contraintes sur a et b:
 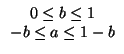 |
(14) |
L'ensemble des trajectoires possibles entre l'instant t et l'instant t+d (h pas de temps) est donc généré par l'ensemble des couples (a,b) vérifiant l'équation 3.1 (figure 3.2). Or, si on connaît la valeur de b (resp. a), on peut déterminer l'intervalle dans lequel a (resp. b) évolue. Nous avons choisi de prendre la valeur de b comme référent: donc, lorsqu'on choisit une valeur de b dans l'intervalle [0,1], les valeurs extrêmes de a sont déterminées. Dans l'algorithme 2.1, nous avions supposé que b ne pouvait être égal qu'à C0.
Notre problème général est le suivant:
Proposition _s
Connaissant la valeur de d et la largeur l de tous les focus suivant les trajectoires possibles entre l'instant t et l'instant t+d, quelle est la probabilité pour qu'au moins un focus contienne au moins i valeurs (sur h possibles) d'un signal U[0,1] ?
Pour chaque valeur yk reçue à l'instant t+k, nous pouvons fournir une contrainte sur a et b pour déterminer l'ensemble des couples (a,b) générant des ``tuyaux'' de largeur l, passant par le point (k,y) et contenant yk pour l'instant t+k. Voici son expression:
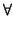 k k 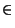 {0, 2,..., h}, yk - {0, 2,..., h}, yk - 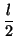 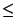 y y 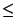 yk + yk + 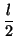 |
|
D'après l'expression de y en fonction de a et b, on a:
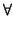 k k 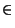 {1, 2,..., h}, {1, 2,..., h}, 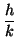 (yk - (yk - 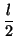 - b) - b) 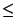 a a 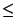 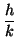 (yk + (yk + 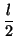 - b) - b) |
|
Pour k=0, on a l'expression particulière:
L'ensemble des contraintes sur a et b, incluant celles données par les inégalités 3.1 se résume par les contraintes Ca, k et Cb, k ci-après:
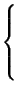 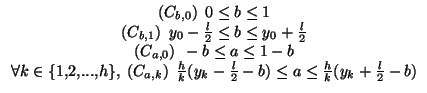 |
(15) |
Le problème 4 revient à trouver la probabilité de pouvoir fixer a et b pour que au moins i contraintes du type Cb, 1 ou Ca, k avec k>0 du système d'inégalités 3.2 soient satisfaites, sachant que les inégalités 3.1 doivent être impérativement satisfaites. À partir de cette expression (ou d'une majoration de cette expression), nous souhaitons montrer des résultats analogues à ceux des propositions 1 et 3, dans le cas où les actions internes produisent un faisceau de droites.
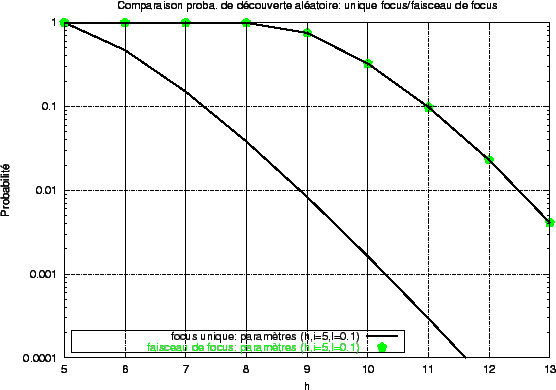
Des calculs expérimentaux de cette probabilité sous-tendent notre supposition 38. Nous constatons que lorsque h, i et l sont fixés, cette probabilité majore celle obtenue pour un unique tuyau, comme on pouvait s'y attendre; on peut même être un peu plus précis en constatant que cette courbe est presque confondue avec celle qui serait obtenue en fixant a priori la valeur des deux points extrêmes (à l'instant t et à l'instant t+d)39. Mais, il est bien évident que l'expérimentation ne permettra ni de prouver l'existence d'un couple (h,i) pour tout l > 0 et tout
 > 0, ni de conditionner correctement les grandeurs h et i lorsque l est fixé et que
> 0, ni de conditionner correctement les grandeurs h et i lorsque l est fixé et que  est très petit (il faudrait largement plus de 1015 essais pour valider statistiquement une valeur de
est très petit (il faudrait largement plus de 1015 essais pour valider statistiquement une valeur de  égale à 10-15 !). Toutefois, on peut constater que:
égale à 10-15 !). Toutefois, on peut constater que:
- le comportement de la probabilité lorsque h varie est identique à celui obtenu pour un unique focus (figure 3.3, partie gauche)
- le comportement de la probabilité lorsque i varie est identique à celui obtenu pour un unique focus (figure 3.3, partie droite)
Or, c'est précisément ce comportement à la limite, lorsque h et/ou i varient, qui a été utilisé lors la démonstration des propositions 1 et 3.
Dans la suite de ce recueil, nous allons supposer qu'une extension des propositions 1 et 3 existe. Pour dimensionner les focus, nous allons utiliser les paramètres h+2,i et l (à  fixé): h, i et l étant les paramètres déterminés pour un unique focus.
fixé): h, i et l étant les paramètres déterminés pour un unique focus.
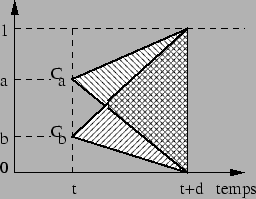
Figure 3.1:
Ensemble des trajectoires rectilignes possibles, entre l'instant t et l'instant t+d
Sur cette figure, on s'est contenté de représenter l'ensemble des trajectoires possibles à partir de seulement deux points Ca et Cb, pris à l'instant t. L'ensemble AR est généré à partir de tous les points Cx, avec
x 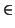 [0, 1]. Sachant que chaque droite D de AR est sensée représenter une possibilité d'évolution du signal réel X, dont les valeurs sont comprises entre 0 et 1, entre l'instant t et l'instant t+d, l'ordonnée de D à l'instant t+d doit être comprise entre 0 et 1, d'où la limitation par les deux cônes présentés sur ce schéma. [0, 1]. Sachant que chaque droite D de AR est sensée représenter une possibilité d'évolution du signal réel X, dont les valeurs sont comprises entre 0 et 1, entre l'instant t et l'instant t+d, l'ordonnée de D à l'instant t+d doit être comprise entre 0 et 1, d'où la limitation par les deux cônes présentés sur ce schéma. |
Figure:
Domaine formé par l'ensemble des couples (a,b) respectant les contraintes de l'équation 3.1
|
|
Figure:
Évolutions comparées de la probabilité de détection d'information à partir d'un signal aléatoire.
|
|




suivant: 2 Évolution de la
monter: 1 Extension du processus
précédent: 1 Extension du processus
Table des matières
Frédéric Davesne
2001-07-13
![$\displaystyle \begin{array}{c} \forall x \in [t,t+d],\:\: f_{a,b}(x)=\frac{a}{d}.(x-t)+b \forall x \in [t,t+d],\:\: f_{a,b}(x) \in [0,1] \end{array}$](img149.gif)
![$\displaystyle \begin{array}{c} \forall x \in [t,t+d],\:\: f_{a,b}(x)=\frac{a}{d}.(x-t)+b \forall x \in [t,t+d],\:\: f_{a,b}(x) \in [0,1] \end{array}$](img149.gif)
![]() > 0, ni de conditionner correctement les grandeurs h et i lorsque l est fixé et que
> 0, ni de conditionner correctement les grandeurs h et i lorsque l est fixé et que ![]() est très petit (il faudrait largement plus de 1015 essais pour valider statistiquement une valeur de
est très petit (il faudrait largement plus de 1015 essais pour valider statistiquement une valeur de ![]() égale à 10-15 !). Toutefois, on peut constater que:
égale à 10-15 !). Toutefois, on peut constater que: