Les graphes temps/signal sont donnés à gauche, alors que les
graphes de droite représentent l'ensemble des valeurs de 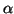 correspondant aux focus dessinés sur les graphes de gauche. Les
génératices sont des droites, déterminées à partir de deux
paramètres a et b (pente et valeur à l'origine). Pour la figure
(b), nous ne représentons les deux focus ``extrêmes'' à gauche;
l'ensemble des valeurs de
correspondant aux focus dessinés sur les graphes de gauche. Les
génératices sont des droites, déterminées à partir de deux
paramètres a et b (pente et valeur à l'origine). Pour la figure
(b), nous ne représentons les deux focus ``extrêmes'' à gauche;
l'ensemble des valeurs de 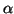 associées à ces focus sont
données, à droite, par le parallélogramme hachuré. associées à ces focus sont
données, à droite, par le parallélogramme hachuré. |
![\includegraphics[]{fig/ex_hough.eps}](img261.png)
![\includegraphics[]{fig/ex_hough.eps}](img261.png)