



suivant: Caractère générique de notre
monter: Algorithme de sélection pour
précédent: Méthode de résolution sélectionnée
Table des matières
Nous utilisons la méthode par découpage d'intervalles. L'algorithme
1.2 que nous présentons ici s'applique à un problème pour
lequel les génératrices sont des fonctions paramétriques, comportant p
paramètres. Nous rappelons que les hypothèses composant la mémoire sont
associées à un unique triplet (h,i,l).
Cet algorithme découle directement de l'algorithme SIVIA
![[*]](file:/usr/lib/latex2html/icons/footnote.png) développé par
Jaulin et Walter. La fonction G est celle décrite dans la
sous-section précédente. Dans la fonction CalculF() décrite dans
l'algorithme, y désigne une boîte incluse dans
développé par
Jaulin et Walter. La fonction G est celle décrite dans la
sous-section précédente. Dans la fonction CalculF() décrite dans
l'algorithme, y désigne une boîte incluse dans
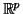 , dont les
composantes suivant les différents axes sont les intervalles
, dont les
composantes suivant les différents axes sont les intervalles
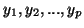 . Dans l'algorithme principal,
. Dans l'algorithme principal, 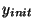 désigne la boîte initiale, qui va être successivement découpée
grâce à la fonction SIVIA(). Celle-ci retourne deux ensembles: le
premier est inclus dans l'ensemble S(t) et l'autre contient S(t)
désigne la boîte initiale, qui va être successivement découpée
grâce à la fonction SIVIA(). Celle-ci retourne deux ensembles: le
premier est inclus dans l'ensemble S(t) et l'autre contient S(t)
![[*]](file:/usr/lib/latex2html/icons/footnote.png) . La fonction Decoupe() découpe une boîte y en deux
boîtes de même volume, selon l'axe portant l'intervalle
. La fonction Decoupe() découpe une boîte y en deux
boîtes de même volume, selon l'axe portant l'intervalle 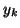 dont la longueur est la plus grande. Les fonctions min et max
désignent respectivement la borne inférieure et la borne
supérieure d'un intervalle. La fonction Largeur appliquée à une
boîte y désigne la longueur du plus petit intervalle
dont la longueur est la plus grande. Les fonctions min et max
désignent respectivement la borne inférieure et la borne
supérieure d'un intervalle. La fonction Largeur appliquée à une
boîte y désigne la longueur du plus petit intervalle 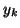 . Le
critère de divisibilité d'une boîte y est désigné par le paramètre
. Le
critère de divisibilité d'une boîte y est désigné par le paramètre
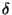 .
.





suivant: Caractère générique de notre
monter: Algorithme de sélection pour
précédent: Méthode de résolution sélectionnée
Table des matières
2002-03-01
