



suivant: Algorithme
monter: Algorithme de sélection pour
précédent: Formalisation de l'ensemble S(t)
Table des matières
Le système 1.1 est très général. Dans le cas où
les fonctions génératrices sont des droites, possédant deux
paramètres a et b (la valeur à l'origine),
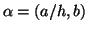 . On
paramètre chaque génératrice par l'équation
. On
paramètre chaque génératrice par l'équation
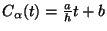 . Le système devient alors:
. Le système devient alors:
![$\displaystyle \left\{ \begin{array}{c}
(I_{D})\:\: b \in [0,1], \:\: a+b \in [...
...\:\: x_{t}-\frac{l}{2}-b \leq a \leq x_{t}+\frac{l}{2}-b\\
\end{array}\right.$](img266.png) |
(8) |
Lorsque i=0 (on désire trouver a et b tels que toutes les inégalités
soient satisfaites), on peut résoudre le problème par la méthode
du simplexe. Mais, lorsque i est non nul, il est plus délicat d'appliquer
cette méthode qui donne une solution respectant l'intégralité des inéquations.
La solution peut être obtenue en considérant l'union des solutions apportées
à des systèmes de h-k inéquations, pour k variant de 0 à i: le nombre de
système à résoudre est donc égal à
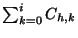 , qui peut être
très important. D'autre part, la méthode du simplexe ne s'applique que
si l'expression des
, qui peut être
très important. D'autre part, la méthode du simplexe ne s'applique que
si l'expression des
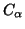 est linéaire. Pour toutes ces raisons,
il nous faut une autre méthode.
est linéaire. Pour toutes ces raisons,
il nous faut une autre méthode.
La première solution est d'effectuer un maillage du domaine des
vecteurs 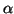 valides, indiqué par la relation (
valides, indiqué par la relation (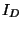 ). Pour
chaque point de ce maillage, on peut alors vérifier le nombre de relations
satisfaites et déduire de cela l'ensemble des points satisfaisant nos
contraintes. Mais, cette solution présente des inconvénients: il est difficile
a priori de connaître la grosseur du maillage à appliquer: si celui-ci
est trop fin, le nombre de points à tester explose suivant le nombre de
dimensions du vecteur
). Pour
chaque point de ce maillage, on peut alors vérifier le nombre de relations
satisfaites et déduire de cela l'ensemble des points satisfaisant nos
contraintes. Mais, cette solution présente des inconvénients: il est difficile
a priori de connaître la grosseur du maillage à appliquer: si celui-ci
est trop fin, le nombre de points à tester explose suivant le nombre de
dimensions du vecteur 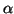 , mais si celui-ci est trop grossier, on
risque de perdre des solutions.
, mais si celui-ci est trop grossier, on
risque de perdre des solutions.
Il existe une méthode qui est particulièrement bien adaptée à
notre problématique: il s'agit d'utiliser les propriétés du calcul
sur les intervalles ![[*]](file:/usr/lib/latex2html/icons/footnote.png) et d'exprimer l'équation 1.1 sous
la forme d'un problème d'inversion ensembliste, qui peut
être mis sous la forme générique suivante:
et d'exprimer l'équation 1.1 sous
la forme d'un problème d'inversion ensembliste, qui peut
être mis sous la forme générique suivante:
Le principe de résolution du problème d'inversion ensembliste, lié
au système 1.1, est décrit dans [Jaulin et Walter, 1993]
ou dans [Jaulin et al., 1996]. Dans notre cas, il s'agit de découper
récursivement l'ensemble initial y en boîtes pour lesquelles on va
calculer l'image par f. Voici comment nous choisissons x, y et f:
- y est une boîte incluant l'ensemble des valeurs de
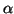 vérifiant la relation (
vérifiant la relation (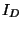 )
)
- x est un intervalle inclus dans [0,h]
- f(y) est un intervalle [min,max] défini de la manière suivante:
min est égal au plus petit nombre de relations de 1.1
satisfaites en considérant l'ensemble des éléments de y, alors que max
est le plus grand nombre de relations satisfaites en considérant
l'ensemble des éléments de y.
Pour calculer f(y), il faut pouvoir inverser chaque relation 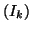 ,
de manière à la mettre sous la forme:
,
de manière à la mettre sous la forme:
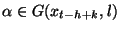 , où G est
une fonction à valeurs dans
, où G est
une fonction à valeurs dans
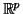 . On associe à
. On associe à 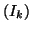 la valeur 1
si
la valeur 1
si
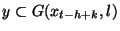 , la valeur 0 si
, la valeur 0 si
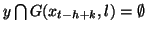 et l'intervalle [0,1] sinon. La somme de ces valeurs donne un intervalle
inclus dans [0,h].
et l'intervalle [0,1] sinon. La somme de ces valeurs donne un intervalle
inclus dans [0,h].
La théorie nous assure qu'on peut classer les boîtes y en trois catégories:
- les boîtes pour lesquelles on est certain que l'intégralité
des points de la boîte vérifient nos contraintes (au moins h-i relations
satisfaites): l'image par f de ces boîtes donne un intervalle [min,max]
tel que min
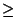 h-i.
h-i.
- les boîtes pour lesquelles on est certain que l'intégralité
des points de la boîte ne vérifient pas nos contraintes (plus de i
relations ne sont pas satisfaites): l'image par f de ces boîtes
donne un intervalle [min,max] tel que max < h-i.
- les boîtes pour lesquelles il existe à la fois des points
vérifiant les contraintes et des points ne vérifiant pas les contraintes:
l'image par f de ces boîtes donne un intervalle [min,max] tel que
min < h-i et max
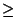 h-i.
h-i.
Le découpage s'effectue sur les boîtes appartenant à la troisième
catégorie. Un critère d'arrêt sur la dimension minimale d'une boîte
permet de maîtriser la précision de l'ensemble S(t) des solutions.
Les quatre points particulièrement intéressants de cette méthode
sont les suivants:
- elle peut gérer les problèmes pour lesquels h-i relations
parmi h doivent être satisfaites
- elle autorise l'utilisation de génératrices
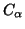 non linéaires
non linéaires
- elle découvre l'intégralité des solutions, même lorsque
l'ensemble des solutions est formé de parties non connexes
- elle permet d'encadrer l'ensemble S(t) par deux ensembles:
l'un est représenté par l'union des boîtes de 1ère catégorie, et
l'autre est formé par l'union des boîtes de la 1ère et de la troisième
catégorie. Le premier ensemble est inclus dans S(t), alors que le
deuxième contient S(t).
Cependant, lorsque la dimension des vecteurs 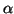 n'est pas
petite (en pratique, inférieure à 5 environ), le nombre de boîtes
créées peut s'accroître énormément, rendant impossible l'inclusion
du calcul de S(t) dans un processus fonctionnant en temps réel.
Cependant, nous avons constaté que, pour une dimension de
n'est pas
petite (en pratique, inférieure à 5 environ), le nombre de boîtes
créées peut s'accroître énormément, rendant impossible l'inclusion
du calcul de S(t) dans un processus fonctionnant en temps réel.
Cependant, nous avons constaté que, pour une dimension de 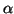 valant 2, la méthode présentée ci-dessus est entre 2 et 4 fois
plus rapide qu'avec une méthode utilisant un maillage comportant
10.000 points
valant 2, la méthode présentée ci-dessus est entre 2 et 4 fois
plus rapide qu'avec une méthode utilisant un maillage comportant
10.000 points ![[*]](file:/usr/lib/latex2html/icons/footnote.png) .
.




suivant: Algorithme
monter: Algorithme de sélection pour
précédent: Formalisation de l'ensemble S(t)
Table des matières
2002-03-01
![$\displaystyle \left\{ \begin{array}{c}
(I_{D})\:\: b \in [0,1], \:\: a+b \in [...
...\:\: x_{t}-\frac{l}{2}-b \leq a \leq x_{t}+\frac{l}{2}-b\\
\end{array}\right.$](img266.png)