



suivant: Contraintes appliquées à la
monter: Conclusion
précédent: Résultats obtenus
Table des matières
L'algorithme 1.2 donne une amélioration certaine par
rapport à un simple maillage de l'espace des vecteurs 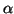 , en
termes de précision de l'ensemble S(t) et de vitesse d'obtention de
S(t). Néanmoins, il reste lourd: pour une valeur de h égale à 100 et
une valeur de i égale à 30 (ce qui signifie que le système
1.1 possède 100 relations
, en
termes de précision de l'ensemble S(t) et de vitesse d'obtention de
S(t). Néanmoins, il reste lourd: pour une valeur de h égale à 100 et
une valeur de i égale à 30 (ce qui signifie que le système
1.1 possède 100 relations 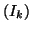 ), on peut
calculer environ une solution S(t) toutes les deux secondes
), on peut
calculer environ une solution S(t) toutes les deux secondes
![[*]](file:/usr/lib/latex2html/icons/footnote.png) . Cela signifie qu'une information perceptive peut être
transmise avec une fréquence maximum de 0.5 Hz. Pour certaines
applications, cela peut être clairement insuffisant. Une amélioration
possible sera la suivante. Si on constate qu'entre les instants t et t+1,
le système 1.1 n'est pas beaucoup modifié
. Cela signifie qu'une information perceptive peut être
transmise avec une fréquence maximum de 0.5 Hz. Pour certaines
applications, cela peut être clairement insuffisant. Une amélioration
possible sera la suivante. Si on constate qu'entre les instants t et t+1,
le système 1.1 n'est pas beaucoup modifié
![[*]](file:/usr/lib/latex2html/icons/footnote.png) (ce qui n'est pas forcément vrai dans le cas général), on peut utiliser
le découpage effectué à l'instant t comme base de calcul à l'instant t+1.
L'idée est de construire un algorithme donnant itérativement l'ensemble
S(t+1) à partir de l'ensemble S(t). Si les différences sont minimes,
il est possible que peu de calculs soient à faire entre ces deux instants,
ce qui pourrait accroître sensiblement la rapidité de l'algorithme.
(ce qui n'est pas forcément vrai dans le cas général), on peut utiliser
le découpage effectué à l'instant t comme base de calcul à l'instant t+1.
L'idée est de construire un algorithme donnant itérativement l'ensemble
S(t+1) à partir de l'ensemble S(t). Si les différences sont minimes,
il est possible que peu de calculs soient à faire entre ces deux instants,
ce qui pourrait accroître sensiblement la rapidité de l'algorithme.
L'algorithme 1.2 peut être également amélioré pour
inclure des groupes d'hypothèses associés chacun à un triplet (h,i,l).
Il n'y a pas a priori de changement profond à effectuer sur
l'algorithme pour obtenir ce résultat plus général. Le moyen le plus
simple est de séparer le calcul de S(t) en autant de calculs associés un
triplet (h,i,l) unique. De la même façon, on peut considérer plusieurs
familles de génératrices. Ainsi, le calcul de S(t) pourrait être généralisé
à une large catégorie de mémoires.
Enfin, il manque un point de travail très important: il s'agit de
comparer les performances du processus de catégorisation face à
celle des techniques existantes. Ce travail n'a pas de
signification pour l'instant, pour les raisons suivantes:
- nous avons autorisé l'existence d'un nombre élevé de degrés de
liberté pour le processus de catégorisation. Dans l'absolu, il semble
possible de trouver ``à la main'' des mémoires permettant de résoudre
des problèmes particuliers.
- mais, on recherche une méthode opérationnelle pour déterminer la
composition de la mémoire, permettant d'éviter un choix arbitraire de
la mémoire.
Donc, il aurait été possible de montrer des résultats, même de
bons résultats (nous en avons !). Mais, cela aurait simplement
signifié qu'on aurait pu, par tâtonnement, trouver des solutions
satisfaisantes. Mais, ce ``tâtonnement'' est beaucoup trop
empirique: on n'aurait pas su dire pourquoi cela fonctionne.




suivant: Contraintes appliquées à la
monter: Conclusion
précédent: Résultats obtenus
Table des matières
2002-03-01