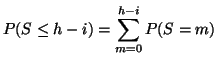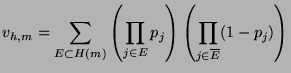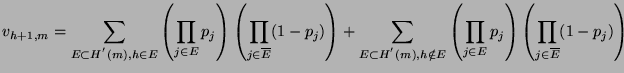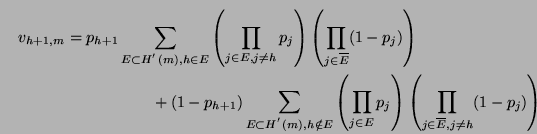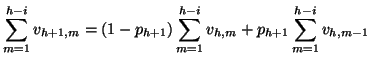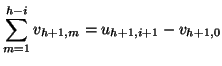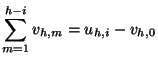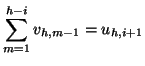Fiabilité de la détection d'une information perceptive

Dans la démonstration qui suit, nous fixons la valeur de l. Il fait bien se rappeler que les $p_{j}$ dépendent, par construction, de l.
Voici la proposition que nous allons montrer:

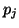
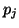
Proposition _s   Si tous les $p_{j}$ sont strictement positifs, alors il existe un ensemble de triplets (h,i,l) tel que l'événement ``Il n'y a pas de détection de l'information perceptive'' est rare. Cet ensemble possède une borne inférieure pour i qui dépend des $p_{j}$, telle que pour tout i supérieur à celle-ci, on peut trouver un h tel que (h,i,l) réponde à notre exigence de rareté. 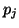Lorsque i est fixé, l'ensemble des h possède une borne supérieure qui dépend également des $p_{j}$, telle que pour tout h inférieur à celle-ci, le triplet (h,i,l) répond à notre exigence de rareté.

La notion de rareté sera interprétée à partir d'un réel $\epsilon \in ]0,1[$ fixé a priori.
La probabilité d'occurrence de l'événement ``Il n'y a pas de détection de l'information perceptive'' est égale à P( S < h-i). Par définition, cet événement est déclaré rare si P( S < h-i) < $\epsilon$. C'est là notre point de départ.
P( S < h-i) s'écrit:

$$P(S \leq h-i) = \sum_{m=0}^{h-i}P(S = m)$$

Les probabilités $P(S \leq h-i)$ et $P(S = m)$ dépendent respectivement de h et i, puis de h et m. Nommons-les respectivement $u_{h,i}$ et $v_{h,m}$ et considérons les suites à deux indices $(u_{h,i})$ et $(v_{h,m})$.
Nous utilisons la propriété d'indépendance des $B_{j}$ pour formuler l'expression générale de $v_{h,m}$:

$$v_{h,m} = \sum_{E \subset H(m)}\left(\prod_{j \in E}p_{j}\right) \left(\prod_{j \in \overline{E}}(1 - p_{j})\right)$$

Avec $H(m)$ ensemble des parties de $\{0,1,...,h-1\}$ comportant $m$ éléments, et $\overline{E}$ ensembles des éléments de $\{0,1,...,h-1\}$ n'appartenant pas à $E$.
La démarche de notre démonstration est la suivante:

1. trouver une relation de récurrence liant les $v_{h,m}$
2. en déduire une relation de récurrence liant les $u_{h,i}$
3. à partir du point précédent, montrer que:
   1. si on fixe a priori un $\epsilon \in ]0,1]$, il existe un $i_{min}$ tel que $u_{i_{min},i_{min}} \leq \epsilon$
   2. la suite $(u_{h,i})$ est croissante suivant h, lorsque i est fixé, et elle tend vers 1 lorsque h tend vers l'infini.
   3. à partir de ce dernier point, on en déduit l'existence de $h_{max}$.

Nous pouvons décomposer la somme $v_{h+1,m}$ en deux sommes, l'une comportant des ensembles E possédant le dernier élément h, et l'autre ne le possédant pas:

$$v_{h+1,m} = \sum_{E \subset H^{'}(m), h \in E} \left(\prod_{j \i... ...\prod_{j \in E}p_{j}\right) \left(\prod_{j \in \overline{E}}(1 - p_{j})\right)$$

Comme h fait partie de E dans la première expression de cette relation, le terme $p_{h+1}$ fait partie du produit $\prod_{j \in E}p_{j}$ et on peut le mettre en facteur. De même, comme h ne fait pas partie de E dans la seconde expression, le terme $1 - p_{h+1}$ peut être mis en facteur dans le produit $\prod_{j \in \overline{E}}(1 - p_{j})$. Ce qui donne la relation suivante:

$$\begin{multline*} v_{h+1,m} = p_{h+1} \sum_{E \subset H^{'}(m), h \in E} \left... ... \left(\prod_{j \in \overline{E}, j \neq h}(1 - p_{j})\right) \end{multline*}$$

Or, l'expression $\sum_{E \subset H^{'}(m), h \in E} \left(\prod_{j \in E, j \neq h}p_{j}\right) \left(\prod_{j \in \overline{E}}(1 - p_{j})\right)$ est exactement la même que $v_{h,m-1}$.
De même, l'expression $\sum_{E \subset H^{'}(m), h \notin E} \left(\prod_{j \in E}p_{j}\right) \left(\prod_{j \in \overline{E}, j \neq h}(1 - p_{j})\right)$ vaut $v_{h,m}$. Ce qui donne le relation de récurrence suivante:

$$v_{h+1,m} = (1 - p_{h+1}) v_{h,m} + p_{h+1} v_{h,m-1}$$ (21)

Si on effectue la somme des éléments de la relation B.11 pour $m \in \{1,...,h-i\}$, on obtient la relation suivante:

$$\sum_{m=1}^{h-i}v_{h+1,m} = (1 - p_{h+1}) \sum_{m=1}^{h-i}v_{h,m} + p_{h+1} \sum_{m=1}^{h-i}v_{h,m-1}$$

Or, pour tout couple $(h,i)$, avec $0 \leq i \leq h$, $\sum_{m=0}^{h-i}v_{h,m} = u_{h,i}$.
On en déduit les trois relations suivantes, par des changements d'indices appropriés:

$$\sum_{m=1}^{h-i}v_{h+1,m} = u_{h+1,i+1} - v_{h+1,0}$$

$$\sum_{m=1}^{h-i}v_{h,m} = u_{h,i} - v_{h,0}$$

$$\sum_{m=1}^{h-i}v_{h,m-1} = u_{h,i+1}$$

Or, $v_{h+1,0} = \prod_{j \in \{0,..,h\}}(1 - p_{j+1}) = (1 - p_{h+1}) v_{h,0}$. Ce qui donne la relation:

$$u_{h+1,i+1} = (1 - p_{h+1}) u_{h,i} + p_{h+1} u_{h,i+1}$$ (22)

Comme $u_{h,i} = u_{h,i+1} + v_{h,i+1}$ et que $v_{h,i+1}$ est un terme positif ou nul, on en déduit que $u_{h,i+1} \leq u_{h,i}$. Or, $p_{h+1}$ est une probabilité, donc est compris dans l'intervalle [0,1]. Par conséquent, la relation B.12 est une relation barycentrique et implique l'inégalité suivante:

$$\forall (h,i), h \geq i \geq 0, u_{h,i+1} \leq u_{h+1,i+1} \leq u_{h,i}$$

On en déduit que lorsque i est fixé, strictement positif, la suite $(u_{h,i})$ est croissante suivant h. Par conséquent, $\forall h \geq i, u_{h,i} \geq u_{i,i}$. Or, $u_{i,i} = \prod_{j=1}^{i}(1 - p_{j})$. Comme on suppose, par hypothèse, que l'ensemble des $p_{j}$ peut être minoré par un $p_{min}$ strictement positif (ce qui signifie que la probabilité d'être à l'intérieur d'un segment de largeur l n'est jamais nulle), $u_{i,i}$ est strictement décroissante et tend vers 0 lorsque i tend vers l'infini. Ce qui signifie que si on fixe a priori un $\epsilon \in ]0,1]$, il existe un $i_{min}$ tel que $u_{i_{min},i_{min}} \leq \epsilon$.
D'autre part, si on choisit un $i \geq i_{min}$, on a également $u_{i,i} \leq \epsilon$, d'après la remarque sur la décroissance de $(u_{i,i})$.
Nous allons à présent montrer que la suite $(u_{h,i})$ tend vers 1 suivant h, lorsque i est fixé.
Nous avons déjà remarqué que la suite $(u_{h,i})$ est croissante suivant h, lorsque i est fixé. Or, les $u_{h,i}$ sont des probabilités, donc $(u_{h,i})$ est majorée par 1. Par conséquent, $(u_{h,i})$ converge suivant h, lorsque i est fixé. Soit $l_{i} = \lim _{h\rightarrow \infty } u_{h,i}$ et $l_{i+1} = \lim _{h\rightarrow \infty } u_{h,i+1}$. La convergence ainsi que la croissance de $u_{h,i}$ suivant h, lorsque i est fixé, permettent d'affirmer:

$$\forall \alpha>0, \exists h_{0} \in \mathbb{N}, \forall h \geq h_{0}, l_{i} - u_{h,i} < \alpha \, \, et \, \, l_{i+1} - u_{h,i+1} < \alpha$$

Comme $(u_{h,i+1})$ est décroissante suivant i, à h fixé, $u_{h,i+1} \leq u_{h,i}$, $l_{i} - u_{h,i} < \alpha \Rightarrow l_{i} - u_{h,i+1} < \alpha$. Or, d'après la relation B.12, $u_{h,i+1} \in [u_{h-1,i+1}, u_{h-1, i}]$. Par conséquent, $l_{i} - u_{h,i+1} \in [l_{i} - u_{h-1,i}, l_{i} - u_{h-1, i+1}]$. Comme $l_{i} - u_{h-1,i} \geq 0$, on en déduit l'encadrement:

$$0 \leq l_{i} - u_{h,i+1} < \alpha$$

En d'autres termes, cela étant vrai pour tout $\alpha$, $l_{i} = \lim _{h\rightarrow \infty } u_{h,i+1} = l_{i+1}$.
Nous venons donc de montrer que pour tout i fixé, $\lim _{h\rightarrow \infty } u_{h,i} = l_{i} = l_{i-1} = ... = l_{0}$.
Or, $u_{h,0} = 1$ pour tout h. Ce qui montre $\lim _{h\rightarrow \infty } u_{h,i} = 1$ pour tout i.
Par conséquent, pour i fixé tel que $i \geq i_{min}$, il existe un $h_{max}$ tel que:

$$\forall h \geq h_{max},\, u_{h,i} \leq \epsilon \, \, et \, \, u_{h_{max + 1},i} > \epsilon$$

Nous venons donc de délimiter l'ensemble des triplets (h,i,l) pour lesquels l'événement ``Il n'y a pas de détection de l'information perceptive'' est rare.