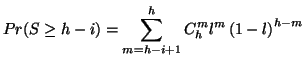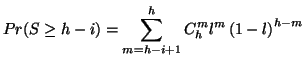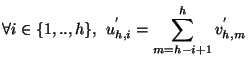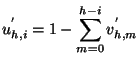Preuve de la proposition 9

Voici la proposition que nous souhaitons montrer.

Proposition _s   L'ensemble des triplets (h,i,l) permettant au système de respecter CO est non vide. Cet ensemble peut être caractérisé de la manière suivante: pour tout l fixé, l'ensemble des (h,i) permettant le respect de CO est non vide. De plus les valeurs de h de cet ensemble possèdent une borne inférieure dépendant de l, telle que pour tout h supérieur à celle-ci, on peut trouver un i pour que (h,i,l) respecte CO.

Nous reprendrons les notations utilisées dans la sous-section précédente.
La contrainte CO impose que la détection d'une information perceptive en sortie du système soit un événement rare. Nous considérons un signal X dont chaque $B_{j}$ suit une loi uniforme sur [0,1] et le $X_{d}$ vaut 0. Nous savons que le volume de l'ensemble des h-échantillons $b_{1},b_{2},...,b_{h}$ générés à partir de X est égal à 1, qui correspond au volume de l'ensemble des h-échantillons générés à partir de l'ensemble de tous les signaux possibles. Comme la contrainte CO peut se traduire en termes de calcul de volume de l'ensemble des solutions en sortie du système, on en déduit que notre démonstration ne changera pas si on considère un unique signal X, associés aux $B_{j}$ que nous venons de définir. Or, la probabilité d'occurrence de l'événement ``Une information perceptive est détectée'' est égale à P($S \ge h-i$). Dans le cas particulier de ce X, les $p_{j}$ obtenues à partir des $B_{j}$ sont égaux et valent l. Le calcul de P($S \ge h-i$) est donc facilité par rapport à la sous-section précédente, car la loi de S est binomiale, de paramètres h et l. Il vient:

$$Pr(S \geq h-i) = \sum_{m=h-i+1}^{h}C_{h}^{m}l^{m}\left(1-l\right)^{h-m}$$

Considérons la suite $(v^{'}_{h,m})$ définie par la relation suivante:

$$\forall m \in \{1,..,h\},\:\:v^{'}_{h,m} = C_{h}^{m}l^{m}\left(1-l\right)^{h-m}$$

Nous définissons la suite $(u^{'}_{h,i})$ en fonction des $v^{'}_{h,m}$:

$$\forall i \in \{1,..,h\},\:\:u^{'}_{h,i} = \sum_{m=h-i+1}^{h}v^{'}_{h,m}$$

Donc, $u^{'}_{h,i} = Pr(T_{S} \geq h-i)$.
Or, sachant que $\sum_{m=0}^{h}v^{'}_{h,m} = 1$, on peut transformer l'expression de $u^{'}_{h,i}$:

$$u^{'}_{h,i} = 1 - \sum_{m=0}^{h-i}v^{'}_{h,m}$$

Or, la suite $(v^{'}_{h,m})$ est un cas particulier de l'étude faite au paragraphe B.3.2, avec des $p_{j}$ tous égaux et valant l . Lorsque i est fixé, on en déduit que:

$$lim_{h \rightarrow \infty} \sum_{m=0}^{h-i}v^{'}_{h,m} = 1$$

Par conséquent, lorsque i est fixé:

$$lim_{h \rightarrow \infty} u^{'}_{h,i} = 0$$

Par conséquent, lorsque $\epsilon > 0$ et i sont fixés, il existe un $h_{min}$ tel que pour tout $h \geq h_{min}$, $Pr(T_{S} \geq h-i) < \epsilon$.