



suivant: Fiabilité de la détection
monter: Preuves concernant la fiabilité
précédent: Preuves concernant la fiabilité
Table des matières
Cette section est consacrée à la preuve de la proposition
7, page ![[*]](file:/usr/lib/latex2html/icons/crossref.png) . Nous allons procéder
par étapes:
. Nous allons procéder
par étapes:
- Montrer qu'il existe des triplets (h,i,l) tels que l'événement
``Il n'y a pas de détection de l'information perceptive'' est rare.
C'est l'objet de la proposition 8, que nous prouverons
dans la sous-section suivante.
- Montrer qu'il existe des triplets (h,i,l) vérifiant CO. C'est
l'objet de la proposition 9 (voir la sous-section B.3.3).
- Donner des conditions suffisantes pour que l'intersection
des deux ensembles soit non vide, ou pour que cette intersection soit vide,
ce qui est l'objectif de cette section. Cela sera fait dans la
sous-section B.3.4.
On considère le h-échantillon (
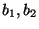 , ...,
, ..., 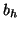 ) formé
à partir des réalisations des variables aléatoires réelles
) formé
à partir des réalisations des variables aléatoires réelles
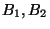 , ...,
, ..., 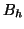 .
. 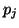 est la probabilité pour que la
réalisation
est la probabilité pour que la
réalisation 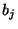 de la variable aléatoire
de la variable aléatoire 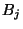 soit dans
l'intervalle [-l/2,l/2]. Cette probabilité est identique à la probabilité
que la valeur
soit dans
l'intervalle [-l/2,l/2]. Cette probabilité est identique à la probabilité
que la valeur 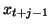 du signal X à l'instant t+j-1 appartienne
au focus. On considère la variable aléatoire discrète
du signal X à l'instant t+j-1 appartienne
au focus. On considère la variable aléatoire discrète 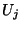 ,
à valeurs dans
,
à valeurs dans 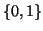 , qui vaut 1 si la réalisation
, qui vaut 1 si la réalisation 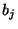 est
dans l'intervalle [-l/2,l/2] et vaut 0 dans le cas contraire.
est
dans l'intervalle [-l/2,l/2] et vaut 0 dans le cas contraire. 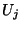 suit une loi de Bernoulli, de paramètre
suit une loi de Bernoulli, de paramètre 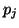 . Enfin, on considère
la variable aléatoire S, à valeurs discrètes dans
. Enfin, on considère
la variable aléatoire S, à valeurs discrètes dans
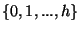 ,
qui représente le nombre de composantes de du h-échantillon
(
,
qui représente le nombre de composantes de du h-échantillon
(
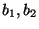 , ...,
, ..., 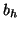 ) comprises dans l'intervalle
[-l/2,l/2]:
) comprises dans l'intervalle
[-l/2,l/2]:
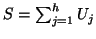 .
.
Dans le cas où les 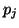 seraient égales, S suivrait une loi
binomiale. Cependant, nous considérons que les
seraient égales, S suivrait une loi
binomiale. Cependant, nous considérons que les 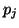 peuvent
avoir des valeurs distinctes.
peuvent
avoir des valeurs distinctes.




suivant: Fiabilité de la détection
monter: Preuves concernant la fiabilité
précédent: Preuves concernant la fiabilité
Table des matières
2002-03-01