



suivant: Conditions de convergence des
monter: Cadre général de l'apprentissage
précédent: Positionnement de l'AR par
Table des matières
Le problème que nous avons brièvement explicité ci-dessus est un
problème d'optimisation. Pour un vecteur d'entrée donné X(t) (perception)
à l'instant t, il s'agit de choisir à tout instant t l'action a(t) qui
maximise l'espérance de la somme des renforcements r(t+k) futurs (dans
un horizon de temps fini ou infini). La technique mathématique sous-jacente
est la programmation dynamique (voir l'article de référence [Bellman, 1957]
ou, pour une vue générale, le livre de Bertsekas [Bertsekas, 1987]): cela
n'est pas surprenant car le problème de maximisation proposé ci-dessus est
décomposable en un problème à l'instant t (choisir la meilleure action à
l'instant t) et en un autre problème (maximiser l'espérance des renforcements
futurs à l'instant t+1); donc, la connaissance, par récursions successives,
des différents sous-problèmes à l'instant t+k, puis t+k-1, ..., puis t+1
permet finalement de résoudre le problème à l'instant t. Mais, celle-ci
n'est appliquable que si on peut connaître parfaitement, à l'instant t,
l'évolution du système par application d'une séquence quelconque d'actions.
Historiquement, l'AR s'est répandue grâce aux travaux précurseurs de Barto
et Sutton au début des années 1980 (voir l'article de référence [Barto et al., 1983]
sur la méthode AHC ![[*]](file:/usr/lib/latex2html/icons/footnote.png) ), puis de
Watkins ([Watkins, 1989]) donnant naissance à la technique du Q-Learning.
Ces deux techniques sont les archétypes de deux classes d'algorithme d'AR:
les algorithmes fonctionnant par itération sur la politique d'actions (AHC)
et les algorithmes cherchant la fonction valeur optimale (Q-Learning, Sarsa
[Rummery, 1995], R-Learning [Schwartz, 1993]), celle-ci influençant
directement le choix de l'action a(t) à tout moment. L'architectures ainsi
que l'algorithme de haut niveau associé au Q-Learning est disponible à
l'annexe A.1.2. Le schéma de haut niveau de l'algorithme
AHC se trouve en annexe (figure A.1, page
), puis de
Watkins ([Watkins, 1989]) donnant naissance à la technique du Q-Learning.
Ces deux techniques sont les archétypes de deux classes d'algorithme d'AR:
les algorithmes fonctionnant par itération sur la politique d'actions (AHC)
et les algorithmes cherchant la fonction valeur optimale (Q-Learning, Sarsa
[Rummery, 1995], R-Learning [Schwartz, 1993]), celle-ci influençant
directement le choix de l'action a(t) à tout moment. L'architectures ainsi
que l'algorithme de haut niveau associé au Q-Learning est disponible à
l'annexe A.1.2. Le schéma de haut niveau de l'algorithme
AHC se trouve en annexe (figure A.1, page ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
).
Les méthodes d'AR basées sur la recherche de la fonction valeur optimale
sont les plus répandues, car elles sont en fait plus simples d'emploi.
Dans ce cadre, le problème est d'évaluer cette fonction valeur. L'idée est
de transformer les équations du problème de programmation dynamique de
manière à résoudre itérativement le problème de PD: cette écriture
itérative se nomme la technique des différences temporelles (TD)
![[*]](file:/usr/lib/latex2html/icons/footnote.png) (voir [Sutton, 1988] pour TD). Cette méthode permet d'estimer la fonction
valeur, sans pour autant connaître un modèle de l'environnement. D'autres
méthodes découlent de TD: on peut citer TD(
(voir [Sutton, 1988] pour TD). Cette méthode permet d'estimer la fonction
valeur, sans pour autant connaître un modèle de l'environnement. D'autres
méthodes découlent de TD: on peut citer TD(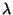 ), qui introduit une
``trace d'éligibilité'' qui va permettre d'influencer la valeur non plus du
dernier état parcouru (à l'instant t), mais l'ensemble des valeurs des états
passés, avec toutefois une atténuation exponentielle de cette modification
(donnée par la valeur
), qui introduit une
``trace d'éligibilité'' qui va permettre d'influencer la valeur non plus du
dernier état parcouru (à l'instant t), mais l'ensemble des valeurs des états
passés, avec toutefois une atténuation exponentielle de cette modification
(donnée par la valeur ![[*]](file:/usr/lib/latex2html/icons/footnote.png) du paramètre
du paramètre 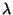 ).
L'algorithme
).
L'algorithme
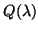 est une extension du Q-Learning original, utilisant
cette trace d'éligibilité ([Peng et Williams, 1996]).
est une extension du Q-Learning original, utilisant
cette trace d'éligibilité ([Peng et Williams, 1996]).
Pour mettre en oeuvre les techniques d'AR, il faut modéliser ce
qui va constituer la ``mémoire'' du système, c'est-à-dire le
support de la fonction valeur. Voici plusieurs possibilités qui
ont été développées dans la littérature, dans le cas où l'espace
d'états est continu ![[*]](file:/usr/lib/latex2html/icons/footnote.png) et où il est confondu avec
l'espace engendré par les signaux d'entrée du système:
et où il est confondu avec
l'espace engendré par les signaux d'entrée du système:




suivant: Conditions de convergence des
monter: Cadre général de l'apprentissage
précédent: Positionnement de l'AR par
Table des matières
2002-03-01