Conditions de convergence des algorithmes d'AR

D'un point de vue théorique, des preuves de convergence de l'algorithme vers une politique de choix d'action optimale n'ont été obtenues que pour les algorithmes utilisant la méthode des différences temporelles (Q-Learning, Sarsa), en faisant l'hypothèse que le processus de décision est modélisable par une chaîne de Markov (MDP), possédant un nombre d'états fini. Le cas où l'espace d'états du système est discret a été traité en premier: le lecteur pourra consulter [Sutton, 1988] et [Dayan, 1992] pour les preuves de convergence de TD(0), puis [Dayan, 1992], [Dayan et Sejnowski, 1994] et [Tsitsiklis, 1994] pour les preuves de convergence de TD(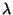$\lambda$). Dans le cas où l'espace d'états est continu, la preuve a été apporté par [Munos, 1997], par découpages successifs de l'espace d'états (triangulation de Delauney).
Dans les autres cas, cités dans la sous-section précédente, il n'y a aucune garantie théorique de convergence, ce qui ne signifie pas que l'apprentissage ne fonctionne pas: historiquement, l'exemple le plus spectaculaire est fourni par le ``joueur'' de backgammon de Tesauro, utilisant une modélisation de la fonction valeur par un réseau de neurones multi-couches [Tesauro, 1994]. Mais, les (nombreux) paramètres peuvent être délicats à fixer, même pour des problème apparemment ``simples'', en particulier lorsque la fonction valeur possède des discontinuités importantes [Bersini et Gorrini, 1996]. [Tsitsiklis et Roy, 1996] montre que dans le cas d'une fonction d'approximation non-linéaire, la méthode TD peut devenir instable. Il en est de même pour le Q-Learning avec fonction d'approximation linéaire [Baird, 1995]. Pendrith souligne aussi la possible difficulté d'appliquer les algorithmes d'AR en robotique mobile ( [Pendrith et McGarity, 1998], [Pendrith, 1999]).