Causes de difficultés dans l'utilisation des algorithmes d'AR

Dans les sous-sections précédentes, nous avons identifié les mécanismes de haut niveau des algorithmes d'AR et présenté le cadre général pour lequel des preuves de convergence ont été établies. En pratique, des difficultés peuvent apparaître dans les cas suivants:

• le temps pour obtenir une solution convenable est prohibitif
• le problème de décision n'est pas markovien
• la fonction valeur est difficile à interpoler

Nous allons développer brièvement les deux premiers points. Pour le dernier, le lecteur pourra se reporter à [Bersini et Gorrini, 1996].
Le premier point est lié au mécanisme d'exploration de l'espace d'états du système, intervenant au moment de choisir l'action à exécuter à l'instant t. Cette problématique est vaste et c'est un des enjeux actuels majeurs dans le domaine de l'AR: le lecteur pourra se reporter à [Wiering, 1999] pour un point de vue complet. En bref, si la nature du problème implique que la probabilité d'atteindre au hasard une solution relativement correcte (qu'on pourra optimiser par la suite) est très faible, le temps (qu'on peut compter en nombre d'essais) pour atteindre cette première solution peut être très important, rendant l'algorithme inutilisable en pratique. Or, dans un problème complexe, l'espace d'états est très souvent grand. Il faut donc guider l'apprentissage. Trois catégories de solutions peuvent être apportées pour réduire cette difficulté:

• découper le problème en sous-problèmes, hiérarchiquement connectés [McGovern et al., 1998],
  [Davesne et Barret, 1999b]
• introduire de la connaissance a priori pour éliminer immédiatement des possibilités visiblement non intéressantes (les travaux portant sur le Q-Learning flou vont dans ce sens [Jouffe, 1997])
• modifier la topologie du modèle du système de manière à ne conserver que les états ``importants'' du système (manière dont on construit les états du système): les méthodes procédant par regroupement d'états vont dans ce sens.

L'hypothèse markovienne est théoriquement essentielle, puisque les résultats de convergence connus jusqu'à présent ne s'appliquent que sur des MDP. Nous rappelons ici que l'hypothèse markovienne impose que la probabilité 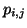$p_{i,j}$ de passage d'un état i à un état j ne dépend que de i; cela signifie que les états du système antérieurement à son arrivée dans i n'interviennent pas dans le calcul de 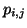$p_{i,j}$. Pratiquement, il est difficile de savoir a priori si le problème, en réalité, est ou n'est pas modélisable par un MDP. En effet, cela dépend principalement de deux catégories de facteurs:

• la pertinence et la ``précision'' des données d'entrée
• la pertinence du choix de la topologie des états par rapport au choix et à la qualité des données d'entrée, mais aussi par rapport à l'objectif de l'apprentissage

Le premier point est évident: les données d'entrée doivent être utilisable pour déduire les états du système, directement (modélisation par une chaîne de Markov) ou indirectement (modélisation par une chaîne de Markov cachée). Le second est moins immédiat. Il traduit la capacité de l'expérimentateur à créer un lien entre la réalité de l'expérience et le modèle théorique dont l'algorithme a besoin pour fonctionner correctement: ce lien se traduit précisément par la construction d'un contexte permettant ce bon fonctionnement; il utilise des connaissances a priori. Prenons l'exemple du problème du pendule inversé pour préciser notre pensée. Si l'objectif est de maintenir le pendule proche de l'équilibre et le chariot proche de son point d'origine, on fera en sorte que la majorité des états du système se trouvent dans cette zone d'équilibre. Mais le degré de cette concentration de l'information est contrebalancé par la qualité des données d'entrée du système (position angulaire et vitesse angulaire de la tige, position et vitesse du chariot): un bruit de mesure trop important rend inefficace une politique de regroupement de l'information, car il existe alors trop d'incertitude sur l'état dans lequel se trouve réellement le système, donc sur l'action correcte à exécuter.
Nos remarques soulignent l'importance du contexte de l'algorithme d'AR, c'est-à-dire de ce qui appartient au savoir-faire de l'expérimentateur. Ce contexte permet de rapprocher la réalité expérimentale et le modèle théorique et tourne autour de la spécification des états du système.