



suivant: Modélisation d'un flux d'erreurs
monter: Outils d'étude de l'incertitude
précédent: Protocole de calcul des
Table des matières
Modélisation du flux d'erreurs dû au contexte d'apprentissage
Dans la suite de ce chapitre, nous effectuerons l'hypothèse
(H) suivante: Le contexte d'apprentissage engendre
un flux d'erreurs qui apparaît lors de l'apprentissage et qui
n'est pas dû à l'algorithme d'AR lui-même.
On considère un système utilisant une politique de commande
apprise grâce à un algorithme d'AR dans un problème de viabilité
![[*]](file:/usr/lib/latex2html/icons/footnote.png) . Nous modélisons l'état de
fonctionnement de ce système par une chaîne de Markov possédant un
état ``viable'', qui correspond à un état de fonctionnement normal
(le système reste dans sa zone de viabilité) et un état
``terminal'' (figure 1.5). On suppose de plus que
l'initialisation du système peut placer celui-ci dans des états
viables de nature différente, connectés chacun à un état terminal
particulier (voir la figure 1.6).
. Nous modélisons l'état de
fonctionnement de ce système par une chaîne de Markov possédant un
état ``viable'', qui correspond à un état de fonctionnement normal
(le système reste dans sa zone de viabilité) et un état
``terminal'' (figure 1.5). On suppose de plus que
l'initialisation du système peut placer celui-ci dans des états
viables de nature différente, connectés chacun à un état terminal
particulier (voir la figure 1.6).
Figure:
Hypothèse de modélisation du flux d'événements ``non-viable''
|
|
Figure:
Modélisation d'un flux d'erreurs possédant deux sources distinctes
|
|
La production d'un événement fâcheux par le système (sortie de la
zone de viabilité) est conditionnée par les valeurs
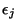 associées à chacune des sources de non-fonctionnement, ainsi que
la probabilité p d'arrivée dans un état de fonctionnement
particulier. Nous allons déterminer l'expression de la durée
moyenne avant la première détection d'erreur (durée de viabilité
moyenne), ainsi que l'écart-type de cette durée (voir le deux
paragraphes qui suivent).
associées à chacune des sources de non-fonctionnement, ainsi que
la probabilité p d'arrivée dans un état de fonctionnement
particulier. Nous allons déterminer l'expression de la durée
moyenne avant la première détection d'erreur (durée de viabilité
moyenne), ainsi que l'écart-type de cette durée (voir le deux
paragraphes qui suivent).




suivant: Modélisation d'un flux d'erreurs
monter: Outils d'étude de l'incertitude
précédent: Protocole de calcul des
Table des matières
2002-03-01
![\includegraphics[]{fig/hyp_sto.eps}](img61.png)