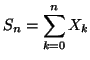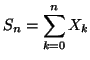suivant: Modélisation d'un flux d'erreurs
monter: Outils d'étude de l'incertitude
précédent: Modélisation du flux d'erreurs
Table des matières
Modélisation d'un flux d'erreurs mono-causal
Nous allons nous intéresser à la modélisation d'un flux
d'erreurs lorsqu'il existe une seule cause d'erreur,
paramétrisée par sa fréquence d'occurrence 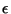 .
.
Considérons un processus dynamique dont l'occurrence d'états
non-viables peut être modélisée par une chaîne de Markov à deux
états V (pour ``viable'') et T (pour ``terminal''): voir la figure
1.5. Il existe trois transitions: l'une de V vers V,
possédant une probabilité de franchissement de
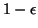 , avec
, avec
![$ \epsilon \in ]0,1[$](img65.png) , une autre de V vers T, possédant une probabilité
de franchissement de
, une autre de V vers T, possédant une probabilité
de franchissement de 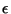 , puis une troisième de T vers V,
possédant une probabilité de transition 1. Cette dernière simule la
réinitialisation du système après l'état terminal.
, puis une troisième de T vers V,
possédant une probabilité de transition 1. Cette dernière simule la
réinitialisation du système après l'état terminal.
À l'instant initial, le processus se trouve dans l'état V. À chaque
pas de temps k, le passage de l'état V à l'état T est formalisé par une
variable aléatoire discrète 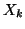 à valeur dans 0,1, suivant une loi
de Bernoulli de paramètre
à valeur dans 0,1, suivant une loi
de Bernoulli de paramètre 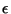 . La valeur de la réalisation
. La valeur de la réalisation 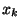 de
de 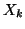 possède la signification suivante: si
possède la signification suivante: si 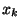 vaut 0, le
processus reste dans l'état V à l'instant k+1, sinon il passe dans l'état
terminal T et, à l'instant k+1, il se retrouve dans l'état V.
vaut 0, le
processus reste dans l'état V à l'instant k+1, sinon il passe dans l'état
terminal T et, à l'instant k+1, il se retrouve dans l'état V.
Nous allons nous intéresser au nombre de pas de temps durant
lesquels le processus reste dans l'état V sans passer par l'état
T. Pour cela, considérons la variable aléatoire discrète
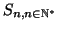 , définie à partir des
, définie à partir des
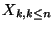 de la manière
suivante:
de la manière
suivante:
La variable aléatoire 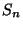 est directement liée à ce nombre de pas
de temps, puisque la réalisation
est directement liée à ce nombre de pas
de temps, puisque la réalisation 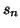 vaut 0 uniquement dans le cas
où le processus est resté dans l'état V pendant n pas de temps.
L'espérance
vaut 0 uniquement dans le cas
où le processus est resté dans l'état V pendant n pas de temps.
L'espérance
![$ E[S_{n}/n]$](img73.png) correspond au nombre moyen d'erreurs par
unité de temps.
correspond au nombre moyen d'erreurs par
unité de temps.
Deux points vont nous intéresser:
- on considère que la valeur de
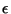 est connue: comment
obtenir la loi de la durée (nombre de pas de temps) séparant deux
passages dans l'état T ?
est connue: comment
obtenir la loi de la durée (nombre de pas de temps) séparant deux
passages dans l'état T ?
- on considère que la valeur de
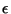 est inconnue: comment
estimer la valeur de
est inconnue: comment
estimer la valeur de 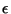 grâce à une réalisation
grâce à une réalisation 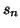 de
de 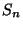 ?
?
Considérons le point 1. Nous allons faire l'hypothèse que les
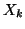 sont indépendantes. Il est connu que
sont indépendantes. Il est connu que 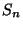 suit une loi
binomiale
suit une loi
binomiale
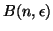 :
:
Le nombre de pas de temps entre l'instant initial et l'instant du
premier passage dans l'état T est une variable aléatoire N
vérifiant:
Les deux événements étant indépendants, il vient:
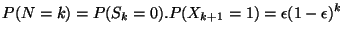 |
(3) |
La probabilité pour que le nombre de pas de temps consécutifs dans
l'état V soit inférieure à n est donc:
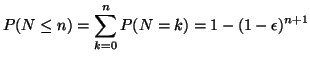 |
(4) |
Considérons à présent le point 2. Calculons en premier lieu
l'espérance et la variance de N grâce à l'équation 1.3.
Il vient (voir l'annexe A.3):
Et
Lorsque 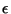 est suffisamment petit, l'écart-type de N est
presque égal à
est suffisamment petit, l'écart-type de N est
presque égal à
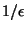 , c'est-à-dire E[N].
, c'est-à-dire E[N].
Si on considère un p-échantillon
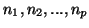 de N,
grâce à la méthode du maximum de vraisemblance, on peut donner un
estimateur
de N,
grâce à la méthode du maximum de vraisemblance, on peut donner un
estimateur
 (voir l'annexe
A.4):
(voir l'annexe
A.4):
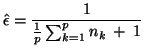 |
(5) |
L'échantillon nous permettra d'établir un histogramme de la
fonction de répartition réelle des durées de viabilité pour le
comparer graphiquement avec la fonction de répartition théorique
utilisant l'estimation de 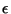 comme paramètre. Un exemple
de fonction de répartition de N est donnée par la figure
1.7, pour
comme paramètre. Un exemple
de fonction de répartition de N est donnée par la figure
1.7, pour
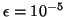 .
.
Figure:
Exemple de fonction de répartition des durées de
viabilité, obtenu pour
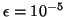
|
|
Voici à présent quelques exemples numériques. Admettons que le
flux d'événements ``non-viables'', issus d'un processus dynamique
en temps discret, soit modélisable en utilisant la variable aléatoire S,
avec un paramètre 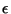 et que le pas de temps vaille 0.02 s. Le
nombre moyen d'erreurs est
et que le pas de temps vaille 0.02 s. Le
nombre moyen d'erreurs est
![$ E[S_{n}] = n \epsilon$](img86.png) . La valeur maximum de
. La valeur maximum de
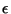 pour qu'il y ait en moyenne une erreur par an est:
pour qu'il y ait en moyenne une erreur par an est:
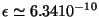 .
.
Si, à présent, on constate qu'un processus n'est jamais passé par
l'état terminal pendant n pas de temps, on peut obtenir une
majoration du nombre moyen d'erreurs par jour, avec une certaine
confiance. Pour une confiance de 0.99, il suffit de déterminer n
pour obtenir P(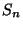 =0) = 0.99 . Pour
=0) = 0.99 . Pour 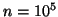 (près de 3
minutes, avec un pas de temps de 0.02 s), on obtient
(près de 3
minutes, avec un pas de temps de 0.02 s), on obtient
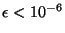 . Grâce à l'expression
. Grâce à l'expression ![$ E[S_{n}]$](img90.png) , on en déduit que la
majoration du nombre d'erreurs moyen par jour est d'environ 4. Si
on voulait garantir que cette majoration soit d'une erreur par an,
il aurait fallu continuer à observer le processus pendant un peu
plus de trois jours.
, on en déduit que la
majoration du nombre d'erreurs moyen par jour est d'environ 4. Si
on voulait garantir que cette majoration soit d'une erreur par an,
il aurait fallu continuer à observer le processus pendant un peu
plus de trois jours.




suivant: Modélisation d'un flux d'erreurs
monter: Outils d'étude de l'incertitude
précédent: Modélisation du flux d'erreurs
Table des matières
2002-03-01