



suivant: Expérimentations autour du problème
monter: Outils d'étude de l'incertitude
précédent: Modélisation d'un flux d'erreurs
Table des matières
Modélisation d'un flux d'erreurs bi-causal dépendant de l'état initial du système
Admettons maintenant qu'il existe deux flux d'erreurs, alimentés
chacun par un type d'erreur: 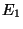 ou
ou 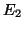 , caractérisés
respectivement par les fréquences d'occurrence d'erreurs
, caractérisés
respectivement par les fréquences d'occurrence d'erreurs
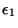 et
et
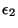 . On suppose que l'initialisation
du système dynamique décide du type de flux d'erreur, suivant
une probabilité p. La figure 1.5 montre la
chaîne de Markov associée à cette modélisation.
. On suppose que l'initialisation
du système dynamique décide du type de flux d'erreur, suivant
une probabilité p. La figure 1.5 montre la
chaîne de Markov associée à cette modélisation.
À partir des résultats de la sous-section précédente (équation
1.3), on en déduit la loi de N:
L'espérance et la variance de N peuvent être facilement déduites
des relations trouvées dans la sous-section précédente:
L'estimation des paramètres
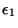 ,
,
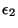 et p
est délicate dans le cas général. Par contre, il existe des cas
simples. Ainsi, si
et p
est délicate dans le cas général. Par contre, il existe des cas
simples. Ainsi, si
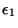 et
et
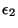 possèdent des
valeurs très éloignées (par exemple,
possèdent des
valeurs très éloignées (par exemple,
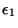 est bien plus
petit que
est bien plus
petit que
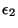 , la fonction de répartition des durées de
viabilité est séparable en deux zones bien distinctes: la figure
1.8 montre le cas où
, la fonction de répartition des durées de
viabilité est séparable en deux zones bien distinctes: la figure
1.8 montre le cas où
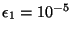 ,
,
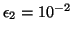 et p=0.5 . On peut affirmer avec une grande
certitude que si le système passe par un état terminal au bout de
moins de 1000 pas de temps, il est très probable que l'erreur soit
et p=0.5 . On peut affirmer avec une grande
certitude que si le système passe par un état terminal au bout de
moins de 1000 pas de temps, il est très probable que l'erreur soit
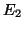 . Au contraire, si le temps de viabilité est supérieur à
1000, il est presque certain que l'erreur soit
. Au contraire, si le temps de viabilité est supérieur à
1000, il est presque certain que l'erreur soit 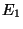 . La
connaissance de ces zones d'influence peut donc permettre
d'estimer les valeurs de
. La
connaissance de ces zones d'influence peut donc permettre
d'estimer les valeurs de
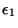 et de
et de
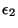 , en
ne tenant compte que des durées de viabilités comprises dans leur
zone d'influence respective.
, en
ne tenant compte que des durées de viabilités comprises dans leur
zone d'influence respective.
Figure:
Exemple de densité de répartition des durées de
viabilité, obtenu pour
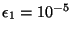 ,
,
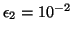 et p=0.5
et p=0.5
|
|




suivant: Expérimentations autour du problème
monter: Outils d'étude de l'incertitude
précédent: Modélisation d'un flux d'erreurs
Table des matières
2002-03-01
![$\displaystyle E[N] = \frac{p}{\epsilon_{1}} + \frac{1-p}{\epsilon_{2}} Var[N] =...
...- \epsilon_{2}}{{\epsilon_{2}}^{2}} +
\frac{p(1-p)}{\epsilon_{1} \epsilon_{2}}$](img95.png)