



suivant: Algorithme d'AO défini dans
monter: Expérimentations autour du problème
précédent: Relation entre et
Table des matières
Le banc d'essai du pendule inversé nous a permis de mettre en
évidence certains mécanismes d'interactions entre l'algorithme d'AR
et son contexte. Dans le cas du pendule inversé, nous avons pu
valider l'hypothèses (H), proposée dans la sous-section 1.3.9.
Nous avons montré que le modèle proposé dans la sous-section
1.3.11 est relativement adapté pour expliquer la répartition
des durées de viabilité au cours d'un apprentissage. L'existence d'une
telle modélisation implique que l'apprentissage ne garantit pas
d'obtenir une politique de commande fiable, et qu'au début d'un essai
d'apprentissage, on ne peut pas prédire la nature de son résultat.
Néanmoins, on peut caractériser statistiquement les performances de
l'apprentissage, en regardant la répartition des durées de viabilité.
Nous avons mis en évidence l'existence de deux zones dans lesquelles
les durées de viabilité sont cantonnées: chaque zone est associée avec une
des deux sources d'erreurs prévues par notre modèle. Nous avons caractérisé
la nature probable des deux sources d'erreurs 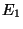 et
et 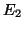 :
: 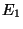 ,
regroupant les essais dont la durée de viabilité est courte
(autour de 150 itérations), est probablement due au paramétrage qui règle
le dilemme exploration/exploitation, alors que la deuxième source d'erreurs
dépend à la fois de la topologie des états du système et de la qualité des
données en entrée de celui-ci.
,
regroupant les essais dont la durée de viabilité est courte
(autour de 150 itérations), est probablement due au paramétrage qui règle
le dilemme exploration/exploitation, alors que la deuxième source d'erreurs
dépend à la fois de la topologie des états du système et de la qualité des
données en entrée de celui-ci.
Nous avons complété les observations de Pendrith (rapport interne
datant de 1994) et modifié certaines conclusions qu'il avait apportées.
En particulier, lorsqu'on augmente beaucoup le nombre d'itérations limite
définissant qu'un apprentissage est réussi, on s'aperçoit que peu d'apprentissages
le sont et que l'ajout d'un bruit de mesure, même faible, empêche systématiquement
la réussite de l'apprentissage.
Enfin, nous avons montré l'utilité des mesures  et
et 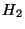 ,
qui permettent effectivement de caractériser la qualité du contexte
d'apprentissage et l'influence (ou le peu d'influence) des variables d'entrée.
Nous avons prouvé l'existence d'un lien grossièrement fonctionnel et bijectif
qui unit
,
qui permettent effectivement de caractériser la qualité du contexte
d'apprentissage et l'influence (ou le peu d'influence) des variables d'entrée.
Nous avons prouvé l'existence d'un lien grossièrement fonctionnel et bijectif
qui unit  et la valeur de
et la valeur de
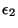 relatif à la deuxième source
d'erreurs:
relatif à la deuxième source
d'erreurs:  = a.log(
= a.log(
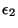 )+b. Ce lien permet, en théorie,
de prévoir l'évolution statistique des durées de viabilité, en connaissant
la nature du bruit de mesure et la valeur de
)+b. Ce lien permet, en théorie,
de prévoir l'évolution statistique des durées de viabilité, en connaissant
la nature du bruit de mesure et la valeur de  , qu'on peut déterminer
avant le début de l'apprentissage: plus
, qu'on peut déterminer
avant le début de l'apprentissage: plus  est faible, et plus
est faible, et plus
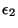 est faible, donc plus la durée de viabilité moyenne est importante. Nous avons
aussi montré, grâce à l'évolution de
est faible, donc plus la durée de viabilité moyenne est importante. Nous avons
aussi montré, grâce à l'évolution de 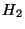 et de
et de  , que la variable
, que la variable
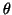 est peu discriminante et qu'on peut découper cet axe moins finement
que ce qui est choisi d'habitude, ce qui n'est pas un résultat évident a priori.
est peu discriminante et qu'on peut découper cet axe moins finement
que ce qui est choisi d'habitude, ce qui n'est pas un résultat évident a priori.
La découverte du lien entre  et la qualité du résultat de
l'apprentissage renforce notre idée de bâtir l'AP dans
l'objectif de minimiser les valeurs de
et la qualité du résultat de
l'apprentissage renforce notre idée de bâtir l'AP dans
l'objectif de minimiser les valeurs de  et de
et de 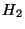 ,
construisant un contexte idéal pour l'AO (c'est-à-dire respectant
la contrainte (
,
construisant un contexte idéal pour l'AO (c'est-à-dire respectant
la contrainte (
 ) ). Le chapitre suivant concerne la
construction de l'AO, utilisant comme hypothèse que le contexte
d'apprentissage respecte la contrainte (
) ). Le chapitre suivant concerne la
construction de l'AO, utilisant comme hypothèse que le contexte
d'apprentissage respecte la contrainte (
 ).
).




suivant: Algorithme d'AO défini dans
monter: Expérimentations autour du problème
précédent: Relation entre et
Table des matières
2002-03-01